题目内容
 如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.
如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.考点:平行线分线段成比例,正方形的性质
专题:证明题
分析:结合条件可得到GF∥AD,则有
=
,由BF∥CD可得到
=
,又因为AD=CD,可得到GF=FB.
| GF |
| AD |
| EF |
| ED |
| BF |
| CD |
| EF |
| ED |
解答:证明:∵四边形ABCD为正方形,
∴BF∥CD,
∴
=
,
∵FG∥BE,
∴GF∥AD,
∴
=
,
∴
=
,且AD=CD,
∴GF=BF.
∴BF∥CD,
∴
| BF |
| CD |
| EF |
| ED |
∵FG∥BE,
∴GF∥AD,
∴
| GF |
| AD |
| EF |
| ED |
∴
| GF |
| AD |
| BF |
| CD |
∴GF=BF.
点评:本题主要考查平行线分线段成比例及正方形的性质,掌握平行线分线段中的线段对应成比例是解题的关键,注意利用比例相等也可以证明线段相等.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
把二次函数y=2x2-4x+3的图象绕原点旋转180°后得到的图象的解析式为( )
| A、y=-2x2+4x-3 |
| B、y=-2x2-4x+3 |
| C、y=-2x2-4x-3 |
| D、y=-2x2+4x+3 |
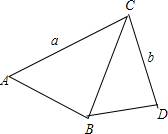 如图所示,已知AB⊥BC,BD⊥CD,AC=a,BC=b.试猜想BD与a,b之间满足怎样的关系时这两个三角形相似?并说明理由.
如图所示,已知AB⊥BC,BD⊥CD,AC=a,BC=b.试猜想BD与a,b之间满足怎样的关系时这两个三角形相似?并说明理由. 如图,在同一时刻的太阳光下,测出垂直于地面长a m的标杆的影长b m,塔的影长c m,这样就可以计算出该塔的高度了.根据上述方法,你可计算出塔的高度是多少米?
如图,在同一时刻的太阳光下,测出垂直于地面长a m的标杆的影长b m,塔的影长c m,这样就可以计算出该塔的高度了.根据上述方法,你可计算出塔的高度是多少米?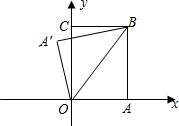 如图,矩形OABC,tan∠AOB=
如图,矩形OABC,tan∠AOB=