题目内容
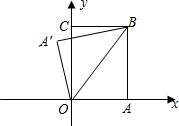 如图,矩形OABC,tan∠AOB=
如图,矩形OABC,tan∠AOB=| 4 |
| 3 |
| k |
| x |
考点:反比例函数综合题
专题:
分析:根据正切值,可得OA、AB的关系,根据勾股定理,可得OA的长,根据翻折的性质,可得OA′与OA的关系,根据倍角三角函数的关系,可得∠AOA′的正切,再根据补角正切间的关系,可得∠A′OE的正切,根据勾股定理,可得A′点的坐标,根据待定系数法,可得函数解析式.
解答:解:如图:作A′E⊥x轴与E点.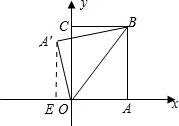 ,
,
由tan∠AOB=
=
,得AB=4x,OA=3x.
由勾股定理,得OA2+AB2=OB2,即(3x)2+(4x)2=102,
解得x=2,3x=6.
由翻折的性质,得OA′=OA=6,∠AOA′=2∠AOB.
tan∠AOA′=tan2∠AOB=
=
=-
.
tan∠A′OE=tan(π-∠AOA′)=-tan∠AOA′=
.
由正切函数值,可设OE=7x,A′E=24x.
由勾股定理,得A′E2+OE2=A′O2,即(7x)2+(24x)2=62.
解得x=
,OE=-
,A′E=
,即A′点的坐标是(-
,
).
反比例函数y=
的图象经过A′,得
k=xy=-
×
=-
.
反比例函数的解析式为y=-
,
故答案为:y=-
.
 ,
,由tan∠AOB=
| AB |
| OA |
| 4 |
| 3 |
由勾股定理,得OA2+AB2=OB2,即(3x)2+(4x)2=102,
解得x=2,3x=6.
由翻折的性质,得OA′=OA=6,∠AOA′=2∠AOB.
tan∠AOA′=tan2∠AOB=
| 2tan∠AOB |
| 1-tan2∠AOB |
2×
| ||
1-(
|
| 24 |
| 7 |
tan∠A′OE=tan(π-∠AOA′)=-tan∠AOA′=
| 24 |
| 7 |
由正切函数值,可设OE=7x,A′E=24x.
由勾股定理,得A′E2+OE2=A′O2,即(7x)2+(24x)2=62.
解得x=
| 6 |
| 25 |
| 42 |
| 25 |
| 144 |
| 25 |
| 42 |
| 25 |
| 144 |
| 25 |
反比例函数y=
| k |
| x |
k=xy=-
| 42 |
| 25 |
| 144 |
| 25 |
| 6048 |
| 625 |
反比例函数的解析式为y=-
| ||
| x |
故答案为:y=-
| ||
| x |
点评:本题考查了反比例函数综合题,利用了翻折的性质,三角函数的倍角关系,勾股定理.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
若x是有理数,则下列各数中一定是正数的是( )
| A、x2+1 |
| B、x2 |
| C、|x| |
| D、|x+1| |
在下列代数式中:-
,
ab,-n,1,
,单项式的个数有( )
| x |
| 2 |
| 2 |
| 2 |
| x |
| A、2个 | B、3个 | C、4个 | D、5个 |
下面各点中,在直线y=-2x上的是( )
| A、(2,1) |
| B、(-1,2) |
| C、(1,2) |
| D、(-2,-1) |
 如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.
如图,延长正方形ABCD的一边CB至E,ED与AB相交于点F,过F作FG∥BE交AE于点G,求证:GF=FB.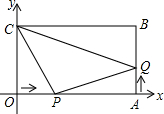 如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上以1厘米/秒的速度沿OA方向作匀速运动,点Q在线段AB上以
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上以1厘米/秒的速度沿OA方向作匀速运动,点Q在线段AB上以 哈西客站投入使用以来,每天输送了大量的旅客.某日,从早8点开始到上午11点,为了缓解旅客压力,在原来基础上新增了3个售票窗口,每个售票窗口售出的车票数y(张)与售票时间x(小时)的关系满足如图所示的图象,其中OA为原有窗口,OB为新增窗口.
哈西客站投入使用以来,每天输送了大量的旅客.某日,从早8点开始到上午11点,为了缓解旅客压力,在原来基础上新增了3个售票窗口,每个售票窗口售出的车票数y(张)与售票时间x(小时)的关系满足如图所示的图象,其中OA为原有窗口,OB为新增窗口.