题目内容
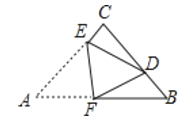
如图,在△ABC中, 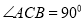 , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则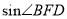 的值为_____________.
的值为_____________.
【答案】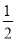
【解析】分析:过点D作DG AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
在Rt△DCE中,由勾股定理求得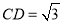 ,所以DB=
,所以DB=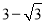 ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得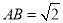 ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得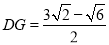 ,
, 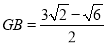 ;
;
设AF=DF=x,则FG= 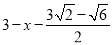 ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程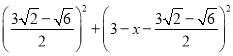 =
=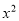 ,解得
,解得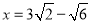 ,从而求得
,从而求得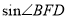 .的值
.的值
详【解析】
如图所示,过点D作DG AB于点G.
AB于点G.
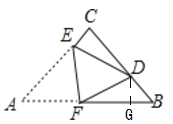
根据折叠性质,可知△AEF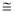 △DEF,
△DEF,
∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得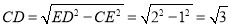 ,
,
∴DB=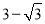 ;
;
在Rt△ABC中,由勾股定理得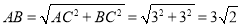 ;
;
在Rt△DGB中, 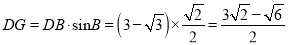 ,
, 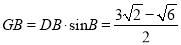 ;
;
设AF=DF=x,得FG=AB-AF-GB=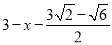 ,
,
在Rt△DFG中, 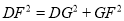 ,
,
即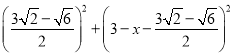 =
=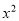 ,
,
解得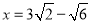 ,
,
∴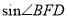 =
=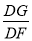 =
=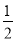 .
.
故答案为: 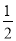 .
.
点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18
规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目


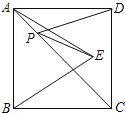
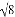 B. 3 C. 4 D. 2
B. 3 C. 4 D. 2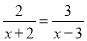
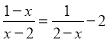
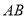 是
是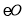 的直径,CD与
的直径,CD与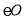 相切于C,
相切于C, 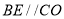 .
.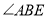 的平分线.
的平分线.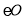 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.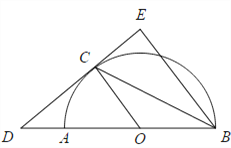
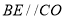 ,推出
,推出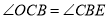 ,由
,由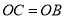 ,推出
,推出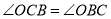 ,可得
,可得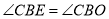 .(2)在
.(2)在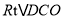 中,求出OD,由
中,求出OD,由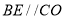 ,可得
,可得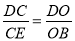 ,由此即可解决问题.
,由此即可解决问题.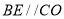 ,
,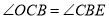 ,
,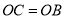 ,
,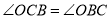 ,
,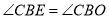 ,
,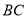 是
是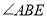 的平分线.
的平分线. 的切线,
的切线,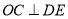 ,即在
,即在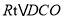 中,DC=8,OC=OA=6,所以
中,DC=8,OC=OA=6,所以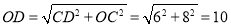 ,
,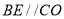 ,
,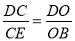 ,
, ,
,
 B.
B.  C.
C.  D.
D. 
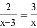 的解为x=_____.
的解为x=_____. ∠A.
∠A. ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).