题目内容
已知正方形的边长为a，其内切圆的半径为r，外接圆的半径为R，则r：R：a=（ ）
A．1：1：
B．1：
：2 C．1：：1 D．：2：4
B【考点】正多边形和圆．
【专题】压轴题．
【分析】经过圆心O作正方形一边AB的垂线OC，垂足是C．连接OA，则在直角△OAC中，∠O=45°．OC是边心距r，OA即半径R．根据三角函数即可求解．
【解答】解：作出正方形的边心距，连接正方形的一个顶点和中心可得到一直角三角形．
在中心的直角三角形的角为360°÷4÷2=45°，
∴内切圆的半径为
，
外接圆的半径为
，
∴r：R：a=1：
：2．
故选B．
【点评】解决本题的关键是构造直角三角形，把半径和边心距用边长表示出来．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
(B)
(C)
(D)
有意义，则点P
在（ ）
；
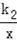
的图象的一个交点是（2，3）．