题目内容
.已知二次函数y=kx2﹣7x﹣7的图象与x轴有两个交点,则k的取值范围为( )
A.k>﹣
 B.k>﹣
B.k>﹣
 且k≠0 C.k≥﹣
且k≠0 C.k≥﹣
 D.k≥﹣
D.k≥﹣
 且k≠0
且k≠0
B【考点】抛物线与x轴的交点.
【专题】计算题.
【分析】根据二次函数的定义得到k≠0,根据.△=b2﹣4ac决定抛物线与x轴的交点个数得到(﹣7)2﹣4k•(﹣7)>0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得
 ,
,
解得k>﹣
 且k≠0.
且k≠0.
故选B.
【点评】本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2﹣4ac决定抛物线与x轴的交点个数:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目

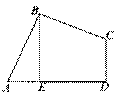
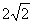 (D)
(D)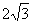
 ㎝,高为
㎝,高为 ㎝,则它的面积为 .
㎝,则它的面积为 .
 B.1:
B.1: