��Ŀ����
20��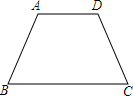 ��ͼ�����ı���ABCD�У�AD��BC��AD=10cm��AB=CD=15cm��sinB=$\frac{4}{5}$����P��Q�ֱ�ӵ�B��Cͬʱ��������P��BC������BC������2cm/s���ٶ��˶�����Q��C��D��A��B������3cm/s���ٶ������˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊxs��
��ͼ�����ı���ABCD�У�AD��BC��AD=10cm��AB=CD=15cm��sinB=$\frac{4}{5}$����P��Q�ֱ�ӵ�B��Cͬʱ��������P��BC������BC������2cm/s���ٶ��˶�����Q��C��D��A��B������3cm/s���ٶ������˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊxs����1����BC�ij���
��2������x��ȡֵ��Χ��
���Ƿ�����ı���APCQΪƽ���ı��Σ������ڣ������ʱx��ֵ���������ڣ���˵�����ɣ�
��3�����CPQ�����Ϊy��cm2������y��x�ĺ�������ʽ����̽��xΪ��ֵʱ����CPQ�����ȡ�����ֵ������������ֵ��
���� ��1����AE��BC���ٸ������Ǻ����͵������ε����ʽ�ɣ�
��2���ٸ��ݵ������ε����ʵó�CD=AB=15��AD=10�����õ�Q��C��D��A��B������3cm/s���ٶ������˶������ó�x��ȡֵ��Χ���ɣ�
�ڸ���ƽ���ı��ε����ʽ��н�ɣ�
��3�����ݷ�$0��x��5��5��x��\frac{25}{3}��\frac{25}{3}��x��\frac{40}{3}$��������ó�����ʽ��ɣ�
��� �⣺��1����AE��BC����ͼ��
�����ı���ABCD�У�AD��BC��AD=10cm��AB=CD=15cm��sinB=$\frac{4}{5}$��
��BE=$15��\frac{3}{5}=9$��
��BC=10+9+9=28cm��
��2���١�BC=28cm����P��BC������BC������2cm/s���ٶ��˶���
������ʱ��Ϊ14s��
�ߵ�Q��C��D��A��B������3cm/s���ٶ������˶���CD+DA+AB=15+10+15=40cm��
������ʱ��Ϊ$\frac{40}{3}$s��
�ɵã�x��ȡֵ��ΧΪ��$0��x��\frac{40}{3}$��
�ڲ������ı���APCQΪƽ���ı��Σ�
�������£�
����Q��AD�ϣ���AQ=PCʱ���ı���APCQΪƽ���ı��Σ�
��AD=10cm��CD=15cm����Q���˶�·��Ϊ3xcm��
��AQ=AD+CD-3x=��25-3x��cm��
��BC=28cm��BP=2xcm��
��25-3x=28-2x��
��ã�x=-3��
��$0��x��\frac{40}{3}$��
������ı���APCQΪƽ���ı��Σ�
��3������Q��CD���˶�ʱ����ͼ2��
��0��x��5ʱ��y=-2.4��x-7��2+117.6��
����Q��AD���˶�ʱ����ͼ3��
��$5��x��\frac{25}{3}$ʱ��y=-12x+168��
����Q��AB���˶�ʱ����ͼ4��
��$\frac{25}{3}��x��\frac{40}{3}$ʱ��y=0.8��3x2-82x+560����
��x=5cmʱ��y=108cm2��
���� ���⿼�����������ʣ�ƽ���ı��κ͵������ε����ʵ�Ӧ�ã�ע�⣺ƽ���ı��εĶԱ���ȣ��������ε�������ȣ�ͬʱע�����ν�ϱ�ʾ����CPQ������ǽ���ؼ���

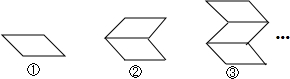
��1�������
| ͼ�α�� | �� | �� | �� | �� | �� | �� |
| �����ĸ��� | 4 | 7 | 10 | 13 | 16 | 19 |
��3���ֱ������15��21��55��ͼ��ʱ����Ҫ���ٸ�������
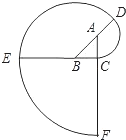 ��ͼ����ABC�ǵ���ֱ�������Σ��ҡ�ACB=90�㣮����CDEF������������ֱ�������εĽ����ߡ������л�CD����DE����EF������Բ�����ΰ�A��B��Cѭ�������AC=1����ô����CDEF�ij���Ϊ��������
��ͼ����ABC�ǵ���ֱ�������Σ��ҡ�ACB=90�㣮����CDEF������������ֱ�������εĽ����ߡ������л�CD����DE����EF������Բ�����ΰ�A��B��Cѭ�������AC=1����ô����CDEF�ij���Ϊ��������| A�� | $\frac{12+7\sqrt{2}}{4}��$ | B�� | $\frac{7+4\sqrt{2}}{4}��$ | C�� | $\frac{5+3\sqrt{2}}{4}��$ | D�� | $\frac{10+5\sqrt{2}}{4}$�� |
 ��ͼ����ABC�У���C=75�㣬����ͼ�����߽�ȥ��C�����1+��2=255�㣮
��ͼ����ABC�У���C=75�㣬����ͼ�����߽�ȥ��C�����1+��2=255�㣮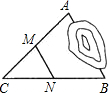 ��ͼ��A��B����������������Ϊ�˲���A��B�����ľ��룬��AB��ѡһ�ʵ��ĵ�C������AC��BC�����ֱ�ȡ�߶�AC��BC���е�E��F�����EF=30m����AB=60m��
��ͼ��A��B����������������Ϊ�˲���A��B�����ľ��룬��AB��ѡһ�ʵ��ĵ�C������AC��BC�����ֱ�ȡ�߶�AC��BC���е�E��F�����EF=30m����AB=60m�� ��ͼ����֪��I�ǡ�ABC�����ģ�AI��BC��D�������ԲO��E����֤��
��ͼ����֪��I�ǡ�ABC�����ģ�AI��BC��D�������ԲO��E����֤��