题目内容
7.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.(1)36和2016这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k和2k-2(其中k取大于1的整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
分析 (1)“神秘数”的定义进行判断即可.
(2)根据平方差公式进行化简运算即可求出答案.
解答 解:(1)36=102-82
故36是神秘数,
2016不能表示为两个连续偶数的平方差,
(2)该神秘数为(2k)2-(2k-2)2
=(2k-2k+2)(2k+2k-2)
=2(4k-2)
=4(2k-1)
故该神秘数为4的倍数.
点评 本题考查平方差公式,解题的关键是正确理解神秘数的定义,本题考查学生的理解能力.

练习册系列答案
相关题目
15.从一个多边形的一个顶点出发,至多可引5条对角线,则该多边形的内角和为( )
| A. | 1620° | B. | 1440° | C. | 1260° | D. | 1080° |

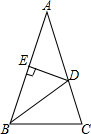 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.