题目内容
3.列不等式解应用题.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少要答对多少道题?
分析 根据小明得分要超过90分,就可以得到不等关系:小明的得分>90分,设应答对x道,则根据不等关系就可以列出不等式求解.
解答 解:设小明答对x道题,
依题意,得10x-5(20-x)>90.
解得$x>12\frac{2}{3}$.
x取最小整数为13.
答:小明至少答对13道题才能超过90分.
点评 此题主要考查了一元一次不等式的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式,正确表示出小明的得分是解决本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
13.关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
| A. | -3<b<-2 | B. | -3<b≤-2 | C. | -3≤b≤-2 | D. | -3≤b<-2 |
11.多项式x2-mxy+9y2能用完全平方因式分解,则m的值是( )
| A. | 3 | B. | 6 | C. | ±3 | D. | ±6 |
15.空气的密度是1.293×10-3g/cm3,用小数把它表示为( )g/cm3.
| A. | 0.1293 | B. | 0.01293 | C. | 0.001293 | D. | 0.0001293 |
12. 如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
 如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )
如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2 |
 在下面的括号内标注理由.
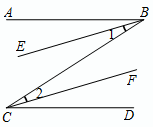
在下面的括号内标注理由. 已知:如图,△CBE是一个锐角三角形,分别以CB,CE为边向外侧作等边三角形ABC和等边三角形CDE,连接AE、BD.
已知:如图,△CBE是一个锐角三角形,分别以CB,CE为边向外侧作等边三角形ABC和等边三角形CDE,连接AE、BD.