题目内容
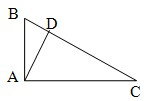
24、如图，∠BAC=90°，△ABC绕点A逆时针旋转得△ADE，点D恰好在BC上，连接CE，问∠BAE与∠DAC有何关系？请说明理由．分析：本题关键是利用旋转性质：图形旋转时，对应点与旋转中心的连线的夹角相等，即旋转角∠BAD=∠CAE．再利用角的和的关系，转化为已知角∠BAC的度数．
解答：解：∵∠BAE=∠BAC+∠CAE，∠BAD=∠CAE，
∴∠BAE+∠DAC=∠BAC+∠BAD+∠DAC=2∠BAC=180°．
答：∠BAE与∠DAC和为180°．
∴∠BAE+∠DAC=∠BAC+∠BAD+∠DAC=2∠BAC=180°．
答：∠BAE与∠DAC和为180°．
点评：本题考查旋转的性质--旋转变化前后，对应角分别相等，把所求角的和转化为已知角．
练习册系列答案
名校课堂系列答案
相关题目
如图，∠BAC=90°，AD⊥BC，△ABE，△ACF都是等边三角形，则S△ABE：S△ACF等于（ ）| A、AB：AC | B、AD2：DC2 | C、BD2：DC2 | D、AC2：AB2 |
6、如图，∠BAC=90°，AD⊥BC，则图中互余的角有（ ）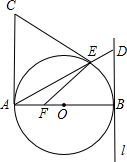
直线AE与l相交于点D．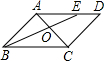
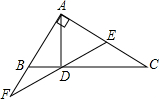
已知：如图，∠BAC=90°，∠C=30°，AD⊥BC于D，DE⊥AB于E，BE=1，BC=