题目内容
4.为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155; B组:155≤x<160; C组:160≤x<165; D组165≤x<170;E组:x≥170)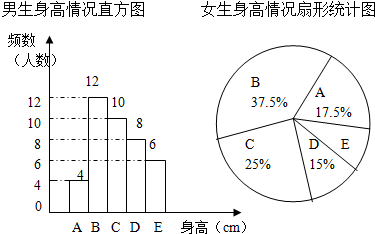
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在B组,中位数在C 组.
(2)样本中,女生的身高在E组的人数有2人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
分析 (1)根据众数和中位数的概念进行解答;
(2)根据男生和女生的人数相等求出女生人数,求出女生的身高在E组的人数的百分比,计算即可;
(3)求出身高在160≤x<170之间女生人数和男生人数即可.
解答 解:(1)男生身高在B组的人数最多,
所以男生的身高众数在B组,
男生人数为4+12+10+8+6=40,
∴中位数是第20和21个数的平均数,所以中位数在C组;
(2)女生的身高在E组的人数为40×(1-17.5%-37.5%-25%-15%)=2人;
(3)400×$\frac{10+8}{40}$+380×40%=332人,
答:身高在160≤x<170之间的学生约有332人.
点评 本题考查的是频数分布直方图,掌握用样本估计总体的方法、正确读懂扇形图的信息、理解中位数和众数的概念是解题的关键.

练习册系列答案
相关题目
19.下列多项式:①x2+y2;②x2-1;③x3+4x-4;④x2-10x+25,其中能直接用公式法因式分解的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.作图题:
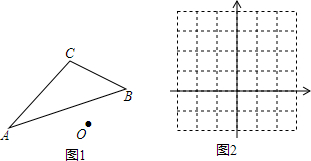
(1)请在图1中作出△ABC关于点O对称的△A′B′C′(不写作法,但要保留作图痕迹)
(2)画二次函数y=$\frac{1}{2}$x2的图象.
解:①列表如下(补充完成下表)
②描点(请在图中描出上表中的点)
③连线(在图中连线,画出y=$\frac{1}{2}$x2的图象)即为所求.

(1)请在图1中作出△ABC关于点O对称的△A′B′C′(不写作法,但要保留作图痕迹)
(2)画二次函数y=$\frac{1}{2}$x2的图象.
解:①列表如下(补充完成下表)
| x | … | -2 | -1 | 0 | 1 | … | |
| y | … | 0.5 | 0 | 0.5 | 2 | … |
③连线(在图中连线,画出y=$\frac{1}{2}$x2的图象)即为所求.
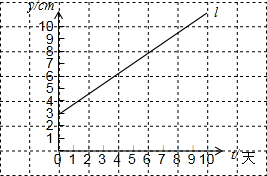 如图,某植物t天后的高度为ycm,l放映了y与t之间的关系,根据图象回答下列问题:
如图,某植物t天后的高度为ycm,l放映了y与t之间的关系,根据图象回答下列问题: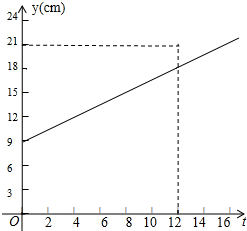 某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题:
某种植物生长t天的高度为y厘米,如图反映了y与t之间的函数关系,请根据图象回答问题: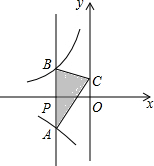 如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5.
如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5.