题目内容
6.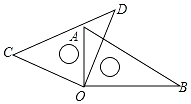 如图,将两块直角三角尺的直角顶点O叠放在一起.
如图,将两块直角三角尺的直角顶点O叠放在一起.(1)若∠AOD=25°,则∠AOC=65°,∠BOD=65°,∠BOC=155°;
(2)比较∠AOC与∠BOD的大小关系,并说明理由;
(3)猜想∠AOD与∠BOC的数量关系,并说明理由.
分析 (1)依据∠AOC+∠AOD=90°,可求得∠AOC的度数,同理可求得∠BOD的度数,然后依据∠BOC=∠COD+∠DOB求解即可;
(2)依据同角的余角相等进行证明即可;
(3)依据∠BOC=∠AOD+∠AOB-∠AOD求解即可.
解答 解:(1)∠AOC=∠COD-∠AOD=90°-25°=65°,
∠BOD=∠AOB-∠AOD=90°-25°=65°,
∠BOC=∠COD+∠DOB=90°+65°=155°
故答案为:65°;65°;155°.
(2)∠AOC=∠BOD.
理由如下:∵∠AOC+∠AOD=90°,∠BOD+∠AOD=90°,
∴∠AOC=∠BOD.
(3)∠AOD+∠BOC=180°.
理由如下:∵∠AOB=∠COD=90°,
∴∠AOB+∠COD=180°,
又∵∠AOB=∠AOD+∠BOD,
∴∠AOD+∠BOD+∠COD=180°.
又∵∠BOD+∠COD=∠BOC,
∴∠AOD+∠BOC=180°.
点评 本题主要考查的是补角和余角的定义,掌握图形相关角的和差关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
 为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )
为了解国家提倡的“阳光体育运动”的实施情况,将某校中的40名学生一周的体育锻炼时间绘制成了如图所示的条形统计图,根据统计图提供的数据,该校40名同学一周参加体育锻炼时间的众数与中位数分别是( )| A. | 8,8 | B. | 8,9 | C. | 9,8 | D. | 10,9 |
14.下列各数中,最大的数是( )
| A. | -$\frac{1}{2}$ | B. | (-$\frac{1}{2}$)2 | C. | (-$\frac{1}{2}$)3 | D. | (-$\frac{1}{2}$)4 |
1.表反映了平面内直线条数与它们最多交点个数的对应关系:
按此规律,6条直线相交,最多有个交点;n条直线相交,最多有$\frac{n(n+1)}{2}$个交点.(n为正整数)
| 图形 | 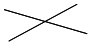 |  | 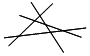 | … |
| 直线条数 | 2 | 3 | 4 | … |
| 最多交点个数 | 1 | 3=1+2 | 6=1+2+3 | … |
16.2015年11月,“喜迎G20•杭州毅行大会”在杭州市民中心盛大开幕,本次毅行大会参与总人数超过42000人,用科学记数法表示42000应为( )
| A. | 42×103 | B. | 4.2×105 | C. | 0.42×105 | D. | 4.2×104 |
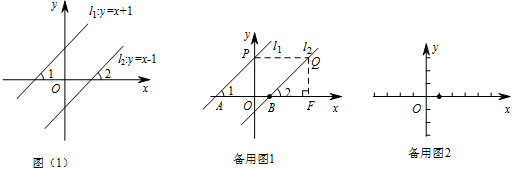
 如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( )
如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( ) 从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是12cm2.
从正面和左面看到长方体的图形如图所示(单位:cm),则从其上面看到图形的面积是12cm2.