题目内容
11．已知△ABC∽△A′B′C′，且对应边的比是2：5，若将△ABC各边都扩大到原来的3倍，△A′B′C′各边长不变，则它们的相似比为6：5．分析 根据题意表示出三角形的一组对应边，进而利用将△ABC各边都扩大到原来的3倍，再表示出对应边的边长，进而得出答案．
解答 解：∵△ABC∽△A′B′C′，且对应边的比是2：5，
∴设一组对应边长为：2x，5x，
∵将△ABC各边都扩大到原来的3倍，
∴该对应边变为：6x，5x，
故则它们的相似比为：6：5．
故答案为：6：5．
点评 此题主要考查了相似三角形的性质，正确表示出对应边长是解题关键．
练习册系列答案
相关题目
1．
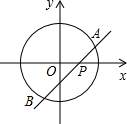如图，在平面直角坐标系中，已知⊙O的半径为2，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（ ）
如图，在平面直角坐标系中，已知⊙O的半径为2，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（ ）| A． | -2≤x≤2 | B． | -2$\sqrt{2}$＜x＜2$\sqrt{2}$ | C． | 0≤x≤2$\sqrt{2}$ | D． | -2$\sqrt{2}$≤x≤2$\sqrt{2}$ |
如图，已知点A，C，B，D在同一条直线上，BE∥DF，∠A=∠F，AB=FD，则图中的全等三角形是△ABE≌△FDC；判定三角形全等的依据是ASA．