题目内容
9.某服装厂计划若干天完成一批夹克衫的订货任务.如果每天生产服装20件,那么就比订货任务少生产100件;如果每天生产23件,那么就可超过订货任务20件.(1)若设原计划x天完成,则这批夹克衫的订货任务用x的代数式可表示为(20x+100)或(23x-20).根据题意列出方程,并求出原计划多少天完成?这批夹克衫的订货任务是多少?
(2)若设这批夹克衫的订货任务为y件,试根据题意列出方程.(直接列出方程,不必求解)
分析 (1)设原计划x天完成,根据“如果每天生产服装20件,那么就比订货任务少生产100件”可得这批夹克衫的订货任务是(20x+100)件;根据“如果每天生产23件,那么就可超过订货任务20件”可得这批夹克衫的订货任务是(23x-20)件;根据这批夹克衫的订货任务不变列出方程,求解即可;
(2)设这批夹克衫的订货任务为y件,根据原计划生产时间不变列出方程即可.
解答 解:(1)若设原计划x天完成,则这批夹克衫的订货任务用x的代数式可表示为(20x+100)或(23x-20);
根据题意,得20x+100=23x-20,
解得:x=40,
所以:20x+100=900(件).
答:原计划40天完成,这批夹克衫的订货任务是900件;
(2)设这批夹克衫的订货任务为y件,根据题意得
$\frac{y-100}{20}$=$\frac{y+20}{23}$.
故答案为(20x+100)或(23x-20).
点评 此题考查一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
20.下列说法正确的是( )
| A. | 1的平方根是1 | B. | 1是算术平方根是±1 | ||
| C. | -1的立方根是-1 | D. | (-1)2的平方根是-1 |
17.一个等腰三角形的两边分别为4cm和10cm,则该等腰三角形的周长为(单位:cm)( )
| A. | 14 | B. | 18 | C. | 24 | D. | 18或24 |
14.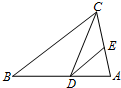 如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
 如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )| A. | △ADE∽△ABC | B. | △ADE∽△ACD | C. | △ADE∽△DCB | D. | △DEC∽△CDB |
19.在平面直角坐标系中,将二次函数y=2x2的图象向上平移2个单位,所得函数图象的解析式为( )
| A. | y=2x2+2 | B. | y=2x2-2 | C. | y=2(x-2)2 | D. | y=2(x+2)2 |