题目内容
17.观察下面解题过程:计算:1+3+5+…+91+93+95.
解:设S=1+3+5+…+91+93+95.…①
则S=95+93+91+…+5+3+1.…②
①+②得
2S=(1+3+5+…+91+93+95)+(95+93+91+…+5+3+1)
=(1+95)+(3+93)+(5+91)+…+(91+5)+(93+3)+(95+1)
=$\frac{(95+1)×48}{2}$
=2304.
(1)仿照上述方法计算:
2+4+6+…+100+102+104
(2)已知n是正整数,且n>10,计算:1+2+3+…+n=$\frac{n(n+1)}{2}$.(只填结果)
分析 (1)仿照所给计算过程设S=2+4+6+…+100+102+104.…①则S=104+102+100…+6+4+2.…②,再计算即可;
(2)仿照所给计算过程计算即可.
解答 解:(1)设S=2+4+6+…+100+102+104.…①
则S=104+102+100…+6+4+2.…②,
①+②得
2S=(2+4+6+…+100+102+104)+(104+102+100…+6+4+2)
=(2+104)+(4+102)+(6+100)+…+(100+6)+(102+4)+(104+2)
=$\frac{(2+104)×52}{2}$
=2756;
(2)设S=1+2+3+…+n.…①
则S=n+(n-1)+(n-2)+…1.…②,
①+②得
2S=(1+2+3+…+n)+[n+(n-1)+(n-2)+…+1]
=(1+n)+(2+n-1)+(3+n-2)+…+(n+1)
=$\frac{n(n+1)}{2}$
故答案为:$\frac{n(n+1)}{2}$.
点评 本题主要考查了数字的变化规律和有理数的混合运算,运用规律是解答此题的关键.

练习册系列答案
相关题目
2. 如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
 如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )| A. | $\sqrt{3}$ | B. | 5 | C. | 3 | D. | $\sqrt{5}$ |
6.若(a-3)2+|b-4|=0,则(a-b)2004的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
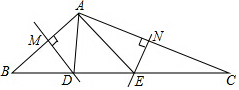 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E. 如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.