题目内容
15.关于x、y的二元一次方程组$\left\{\begin{array}{l}x-y=3\\ 2x+y=9\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=-1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=4\\ y=-1\end{array}\right.$ |
分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x-y=3①}\\{2x+y=9②}\end{array}\right.$,
①+②得:3x=12,
解得:x=4,
把x=4代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
故选C
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:加减消元法与代入消元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)填写下表:
(2)从以下四个方面对甲、乙两城市的空气质量进行分析.
①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些.

(1)填写下表:
| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 85 | 1 |
| 乙 | 80 | 1060 | 80 | 3 |
①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些.
10.不等式组$\left\{\begin{array}{l}{2x+3≥1}\\{\frac{x-1}{2}<1}\end{array}\right.$的整数解的个数是( )
| A. | 0个 | B. | 2个 | C. | 4个 | D. | 5个 |
20.计算:
(1)($\sqrt{3}$+$\sqrt{5}$)($\sqrt{3}$-$\sqrt{5}$)
(2)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$.
(1)($\sqrt{3}$+$\sqrt{5}$)($\sqrt{3}$-$\sqrt{5}$)
(2)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$.
4.某班共有60人参加杜会实践拾棉花劳动,某天,这个班学生拾棉花的数量都在30kg以上,拾棉花的数量具体分组如表所示:
这天这个班学生平均没人拾棉花的数量约是41.3kg.(精确到0.1kg)
| 分组 | 31-35kg | 36-40kg | 41-45kg | 46-50kg | 51-55kg |
| 人数 | 8 | 23 | 15 | 9 | 5 |
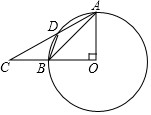 如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.
如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.