题目内容
8.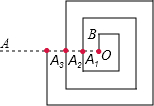 如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,从A2点到A3点的回形线为第3圈,…,依此类推,则第10圈的长为79.
如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、A3….若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,从A2点到A3点的回形线为第3圈,…,依此类推,则第10圈的长为79.
分析 结合图形根据长方形的周长公式计算几个特殊值.
解答 解:观察图形发现:
第一圈的长是2(1+2)+1=7;
第二圈的长是2(3+4)+1=15;
第三圈的长是2(5+6)+1=23;
则第n圈的长是2(2n-1+2n)+1=8n-1.
当n=10时,原式=80-1=79.
故答案为79.
点评 此题主要考查图形变化的规律,结合图形发现:图形的周长正好能转化为长方形的周长再加1.重点分析对应长方形的周长:第n个长方形的长是对应的偶数,宽是对应的奇数.

练习册系列答案
相关题目
16.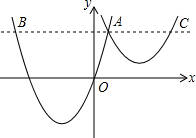 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
3.某中学为筹备校庆,准备印制一批纪念册,每册由4张彩页,6张黑白页构成.印制该纪念册的总费用由制版费和印刷费两部分组成,其中制版费的价格为:彩页300元/张,黑白页50元/张;印刷费用与印数的关系见表:
(1)印制这批纪念册需制版费1500元,印制1千册纪念册的印刷费13000元;
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
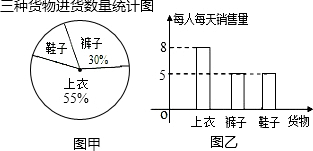
13.某商店在开业前,进了上衣、裤子与鞋子三种货物,其中裤子进了108条,三种货物进货数量的统计图如图甲所示.销售人员(销售上衣3人,销售裤子2人,销售鞋子1人)试销售了3天时间.经统计,这三天里三种货物每人每天销售数量统计图如图乙所示,三种货物3天的销售总量见表格(部分信息未给出).
(1)求所进上衣多少件?鞋子多少双?
(2)把表格补充完整.
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?
| 货物 | 上衣 (件) | 裤子 (条) | 鞋子 (双) |
| 3天的销售总量 | 72 | 30 | 15 |
(2)把表格补充完整.
(3)若销售人员不变,以同样的销售速度销售,请通过计算说明哪种货物最先售完?

3.已知点A(-1,y1),B(2,y2),C(3,y3)都在反比例函数y=-$\frac{5}{x}$的图象上,则下列结论中正确的是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
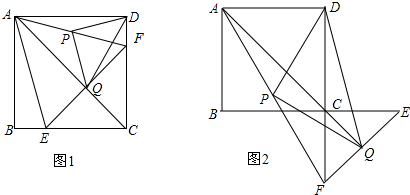
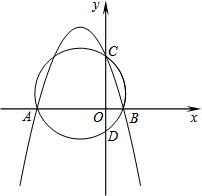 如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.
如图,抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于点A、B,与y轴交于点C.经过A、B、C三点的圆与y轴的负半轴交于点D.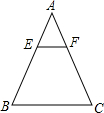 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.