题目内容
解下列分式方程
(1)
+
=4
(2)
=
-1.
(1)
| x |
| 2x-1 |
| 5 |
| 1-2x |
(2)
| 6 |
| x-2 |
| x |
| x+3 |
考点:解分式方程
专题:
分析:(1)根据1-2x=-(2x-1),方程两边可成最简公分母(2x-1),转化成整式方程;
(2)根据方程两边都乘以最简公分母(x-2)(x+3),可转化成整式方程.
(2)根据方程两边都乘以最简公分母(x-2)(x+3),可转化成整式方程.
解答:解:(1)方程两边乘以(2x-1),得
x-5=4(2x-1).
去括号,得
x-5=8x-4,
移项、合并同类项
解得x=-
,
检验:x=-
,2x-1≠0,
x=-
是原分式方程的解;
(2)方程两边都乘以最简公分母(x-2)(x+3),得
6(x+3)=x(x-2)-(x-2)(x+3).
去括号,得
6x+18=x2-2x-x2-3x+2x+6.
解得x=-
,
检验:x=-
时,(x-2)(x+3)≠0,
x=-
是原分式方程的解.
x-5=4(2x-1).
去括号,得
x-5=8x-4,
移项、合并同类项
解得x=-
| 1 |
| 7 |
检验:x=-
| 1 |
| 7 |
x=-
| 1 |
| 7 |
(2)方程两边都乘以最简公分母(x-2)(x+3),得
6(x+3)=x(x-2)-(x-2)(x+3).
去括号,得
6x+18=x2-2x-x2-3x+2x+6.
解得x=-
| 4 |
| 3 |
检验:x=-
| 4 |
| 3 |
x=-
| 4 |
| 3 |
点评:本题考查了解分式方程,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
(3)分式中有常数项的注意不要漏乘常数项.
(2)解分式方程一定注意要验根.
(3)分式中有常数项的注意不要漏乘常数项.

练习册系列答案
相关题目
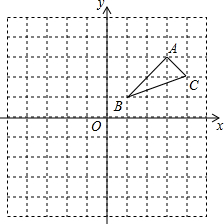 在如图10×10的网格中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图10×10的网格中,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点). 小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)
小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)
 如图是游乐园的一角.
如图是游乐园的一角. 已知一次函数的图象经过(6,-3)和(-3,6)两点,
已知一次函数的图象经过(6,-3)和(-3,6)两点,