题目内容
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
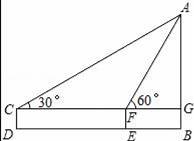

A.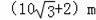
 B.
B.
 C.
C.
 D.
D.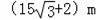

D【考点】解直角三角形的应用-仰角俯角问题.
【分析】利用60°的正切值可表示出FG长,进而利用∠ACG的正切函数求AG长,加上2m即为这幢教学楼的高度AB.
【解答】解:在Rt△AFG中,tan∠AFG=
 ,
,
∴FG=
 =
=
 ,
,
在Rt△ACG中,tan∠ACG=
 ,
,
∴CG=
 =
=
 AG.
AG.
又∵CG﹣FG=30m,
即
 AG﹣
AG﹣
 =30m,
=30m,
∴AG=15
 m,
m,
∴AB=(15
 +2)m.
+2)m.
故选:D.


【点评】考查了解直角三角形的应用﹣仰角俯角问题,构造仰角所在的直角三角形,利用两个直角三角形的公共边求解是常用的解直角三角形的方法.

练习册系列答案
相关题目



 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
 的图象经过点A(1,﹣3),AB垂直x轴于点B,则下列说法正确的是( )
的图象经过点A(1,﹣3),AB垂直x轴于点B,则下列说法正确的是( )

 ,则⊙O的半径为 .
,则⊙O的半径为 .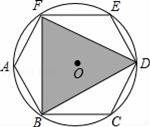

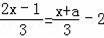
 去分母时,方程右边的﹣2没有乘3,这时方程的解为x=2,试求a的值,并求出原方程正确的解.
去分母时,方程右边的﹣2没有乘3,这时方程的解为x=2,试求a的值,并求出原方程正确的解.