题目内容
在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,则以2.4cm为半径的⊙C与直线AB的关系是 .
相切 .
【考点】直线与圆的位置关系.
【分析】过C作CD⊥AB于D,根据勾股定理求出AB,根据三角形的面积公式求出CD,最后根据直线和圆的位置关系得出即可.
【解答】解:相切,理由是:
过C作CD⊥AB于D,
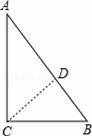

∵在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,
∴由勾股定理得:AB=5cm,
∵由三角形的面积公式得:
 AC×BC=
AC×BC=
 AB×CD,
AB×CD,
∴3×4=5CD,
∴CD=2.4cm,
∴以2.4cm为半径的⊙C与直线AB的关系是相切,
故答案为:相切.
【点评】本题考查了勾股定理,三角形的面积,直线和圆的位置关系的应用,解此题的关键是能正确作出辅助线,并进一步求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
为了估计某市空气质量情况,某同学在30天里做了如下记录:
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 6 | 5 | 1 |
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为 天.

 B.
B.
 C.
C.
 D.
D.


 ,例如2☆3=
,例如2☆3=
 .计算[2☆(﹣4)]×[(﹣4)☆(﹣2)]= .
.计算[2☆(﹣4)]×[(﹣4)☆(﹣2)]= .

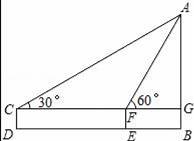

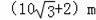
 B.
B.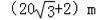
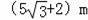
 D.
D.