题目内容
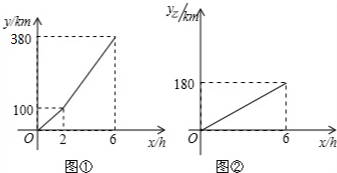
7.在一条笔直的公路上,甲,乙二人从A处同时出发,相背而行,出发段时间后,甲提高了速度,设甲行驶的路程为y甲(单位:km),乙行驶的路程为y乙(单位:km),甲、乙二人之间的距离为y(单位:km),行驶时间为x(单位:h),y与x之间的部分函数图象如图①所示,y乙与x之间的部分函数图象如图②所示.(1)分别求出甲2h,6h行驶的路程;
(2)当0≤x≤6时,求出y甲与x之间的函数关系式,
(3)若6小时后,甲保持第6小时的速度,乙提速,当x=8h时,甲、乙之间的路程相差30km,求乙提速后的速度.
分析 (1)结合图象分析计算,注意图①表示的是甲乙之间的距离(数形结合);
(2)由于甲在途中,速度有变化,故用分段函数来表示(分类讨论);
(3)根据题意找等量关系,列方程求解(方程思想,分类讨论思想)
解答 解:(1)由图①可得,当x=2时,y=100;当x=6时,y=380,
∴甲2h行驶的路程为y-y乙=100-60=40km;
甲6h行驶的路程为y-y乙=380-180=200km.
(2)当0≤x≤6时,分两种情况:
①当0≤x≤2时,设y甲=k1x,
把(2,40)代入y甲=k1x得:2k1=40,
解得:k1=50,
∴y甲=20x;
②当2≤x≤6时,设y甲=k2x+b,
把(2,40),(6,200)代入y甲=k2x+b得:
$\left\{\begin{array}{l}{2{k}_{2}+b=40}\\{6{k}_{2}+b=200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=40}\\{b=-40}\end{array}\right.$,
∴y甲=40x-40.
∴${y}_{甲}=\left\{\begin{array}{l}{20x(0≤x≤2)}\\{40x-40(2≤x≤6)}\end{array}\right.$.
(3)甲第6小时的速度为:(200-40)÷(6-2)=40(km/h),
当x=8h时,甲走的路程为:40×8-40=280km,
设6小时后,乙提速后的速度为xkm/h,当x=8h时,乙走的路程为:180+(8-6)x=180+2x,
当甲走的路程大于乙走的路程,根据题意得:280-(180+2x)=30,
解得:x=35;
当甲走的路程小于乙走的路程,根据题意得:180+2x-520=30,
解得:x=65,
∴乙提速后的速度为35km/h或65km/h.
点评 本题考查了一次函数的应用,解决本题的关键是用待定系数法求函数的解析式,并应用数形结合的解题思想.

| a | 0.000008 | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.02 | 0.2 | 2 | 20 | 200 |
(3)根据你发现的规律填空:
①已知$\root{3}{3}$≈1.442,则$\root{3}{3000}$≈14.42
②已知$\root{3}{0.000456}$≈0.07697,则$\root{3}{456}$≈7.697.
| A. | 购买一张福利彩票,中奖 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 太阳每天从东边升起 | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )| A. | 46° | B. | 44° | C. | 36° | D. | 22° |