题目内容
12.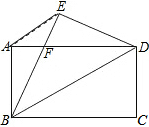 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.(1)求证:BF=DF;
(2)求证:AE∥BD;
(3)若AB=6,AD=8,求BF的长.
分析 (1)由翻折的性质可知∠EBD=∠CBD,由矩形的性质可知:AD∥BC,从而得到∠ADB=∠DBC,于是∠EBD=∠ADB,故此BF=DF;
(2)由BE=AD,BF=FD,可知AF=EF,从而得到∠EAF=∠AEF,然后可证明∠AEF=∠EBD,从而可证明AE∥BD;
(3)在△AFB中利用勾股定理可求得BF的长.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DBC=∠ADB.
由翻折的性质可知:∠DBC=∠EBD,
∴∠ADB=∠EBD.
∴BF=FD.
(2)∵四边形ABCD是矩形,
∴AD=BC.
由翻折的性质可知:BE=BC,
∴AD=BE.
由(1)可知:BF=DF,
∴AF=EF.
∴∠AEB=∠EAF.
∵∠AFE=∠BFD,∠FBD=∠FDB,
∴∠AEB=∠EBD.
∴AE∥BD.
(3)在Rt△ABF中,设BF=FD=x,则AF=8-x,由勾股定理得:AB2+AF2=BF2,即62+(8-x)2=x2.
解得:x=$\frac{25}{4}$.
∴BF的长为$\frac{25}{4}$.
点评 本题主要考查的是翻折的性质、等腰三角形的性质和判定、勾股定理的应用,由翻折的性质找出相等的角或边是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
2.若x轴上的点P到y轴的距离为1,则点P的坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (1,0)或(-1,0) | D. | (0,1)或(0,-1) |
2.已知正比例函数y=kx的图象经过(1,-2)点,则k=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
 在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.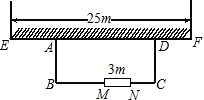 利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.
利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.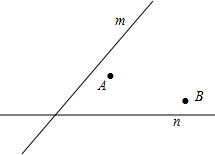 如图,电信部门要在S区修建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?(保留作图痕迹)
如图,电信部门要在S区修建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也必须相等,发射塔应建在什么位置?(保留作图痕迹)