题目内容
17．
如图，△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于$\frac{1}{2}$AC的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为65°．
分析 先根据三角形内角和定理求出∠BAC的度数，再由线段垂直平分线的性质得出∠C=∠CAD，进而可得出结论．
解答 解：∵△ABC中，∠B=55°，∠C=30°，
∴∠BAC=180°-55°-30°=95°．
∵直线MN是线段AC的垂直平分线，
∴∠C=∠CAD=30°，
∴∠BAD=∠BAC-∠CAD=95°-30°=65°．
故答案为：65°．
点评 本题考查的是作图-基本作图，熟知线段垂直平分线的作法是解答此题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
8．已知$\frac{a}{b}=\frac{7}{5}$，则$\frac{a-b}{b}$的值为（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{7}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{2}{5}$ |
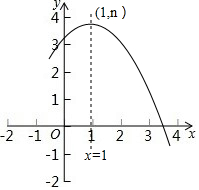二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，其顶点坐标为（1，n），且与x轴的一个交点在（3，0）和（4，0）之间，则下列结论：
12．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
