题目内容
 如图,矩形ABCD的边AD=18cm,AB=16cm,⊙O与AB,BC分别相切于E,F,并且⊙O与以AD为直径的半圆N相切于P,试求⊙O的半径长.
如图,矩形ABCD的边AD=18cm,AB=16cm,⊙O与AB,BC分别相切于E,F,并且⊙O与以AD为直径的半圆N相切于P,试求⊙O的半径长.考点:相切两圆的性质
专题:
分析:如图,作辅助线;首先证明AQ=OE=μ;BE=OF=μ;求出λ=
AD=9,得到NQ=9-μ,OQ=16-μ,ON=9+μ;运用勾股定理列出关于μ的方程,求出μ即可解决问题.
| 1 |
| 2 |
解答:
 解:如图,连接OE、OF;连接ON;
解:如图,连接OE、OF;连接ON;
延长FO交AD于点Q;设⊙O、⊙N的半径分别为λ、μ;
∵⊙O与AB,BC分别相切于E,F,且⊙O与半圆N相切于P,
∴OE⊥AB、OF⊥BC、ON过点P;
∵四边形ABCD为矩形,
∴∠A=∠B=90°,四边形ABFQ、EBFO均为矩形,
∴AQ=OE=μ;BE=OF=μ;由题意得:λ=
AD=9,
∴NQ=9-μ,OQ=16-μ,ON=9+μ;
由勾股定理得:(9+μ)2=(9-μ)2+(16-μ)2,
解得:μ=4或64(设去),
即⊙O的半径长=4(cm).
 解:如图,连接OE、OF;连接ON;
解:如图,连接OE、OF;连接ON;延长FO交AD于点Q;设⊙O、⊙N的半径分别为λ、μ;
∵⊙O与AB,BC分别相切于E,F,且⊙O与半圆N相切于P,
∴OE⊥AB、OF⊥BC、ON过点P;
∵四边形ABCD为矩形,
∴∠A=∠B=90°,四边形ABFQ、EBFO均为矩形,
∴AQ=OE=μ;BE=OF=μ;由题意得:λ=
| 1 |
| 2 |
∴NQ=9-μ,OQ=16-μ,ON=9+μ;
由勾股定理得:(9+μ)2=(9-μ)2+(16-μ)2,
解得:μ=4或64(设去),
即⊙O的半径长=4(cm).
点评:该题主要考查了相切两圆的性质、矩形的判定及其性质、勾股定理等几何知识点及其应用问题;解题的关键是作辅助线,对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
 如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )
如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )| A、6cm | B、8cm |
| C、10cm | D、4cm |
下列方程为一元一次方程的是( )
| A、x+3=0 | ||
| B、x+2y=3 | ||
| C、x2=2x | ||
D、
|
下列说法中不正确的是( )
| A、最小的正整数是1 |
| B、最大的负整数是-1 |
| C、有理数分为正数和负数 |
| D、绝对值最小的有理数是0 |
 如图,正方形ABCD被分成两个小正方形和两个长方形,如果两个小正方形的面积分别是6cm2和2cm2,那么两个长方形的面积和为
如图,正方形ABCD被分成两个小正方形和两个长方形,如果两个小正方形的面积分别是6cm2和2cm2,那么两个长方形的面积和为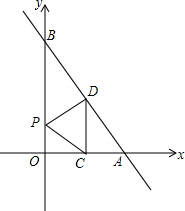 一次函数y=kx+b的图象与x轴、y轴分别交于点A(2,0),B(0,4),O为坐标原点,线段OA、AB的中点分别为点C、D,P为直线OB上一动点.
一次函数y=kx+b的图象与x轴、y轴分别交于点A(2,0),B(0,4),O为坐标原点,线段OA、AB的中点分别为点C、D,P为直线OB上一动点. 如图,AC和BD相交于点O,OA=OC,OB=OD,DC与AB平行吗?为什么?
如图,AC和BD相交于点O,OA=OC,OB=OD,DC与AB平行吗?为什么?