题目内容
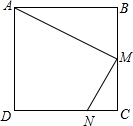 如图,在正方形ABCD中,M是BC边上的一个动点,N在CD上,且CN=
如图,在正方形ABCD中,M是BC边上的一个动点,N在CD上,且CN=| 1 |
| 4 |
考点:相似三角形的判定
专题:
分析:先根据BM=x得出CM=4-x,再由CN=
CD得出CN=1,再分△ABM∽△MCN与△ABM∽△NCM两种情况进行讨论.
| 1 |
| 4 |
解答:解:∵在正方形ABCD中,AB=4,
∴AB=BC=CD=4,
∵BM=x,
∴CM=4-x.
∵CN=
CD,
∴CN=1.
当△ABM∽△MCN时,、
=
,即
=
,解得x=2;
当△ABM∽△NCM时,
=
,即
=
,解得x=
.
综上所述,当x=2或
时,以A、B、M为顶点的三角形和以N、C、M为顶点的三角形相似.
故答案为:2或
.
∴AB=BC=CD=4,
∵BM=x,
∴CM=4-x.
∵CN=
| 1 |
| 4 |
∴CN=1.
当△ABM∽△MCN时,、
| AB |
| CM |
| BM |
| CN |
| 4 |
| 4-x |
| x |
| 1 |
当△ABM∽△NCM时,
| AB |
| CN |
| BM |
| CM |
| 4 |
| 1 |
| x |
| 4-x |
| 16 |
| 5 |
综上所述,当x=2或
| 16 |
| 5 |
故答案为:2或
| 16 |
| 5 |
点评:本题考查的是相似三角形的判定定理,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
 如图,已知正方形ABCD的边长为8,点E,F分别在边BC、CD上,∠EAF=45°.当EF=8时,△AEF的面积是( )
如图,已知正方形ABCD的边长为8,点E,F分别在边BC、CD上,∠EAF=45°.当EF=8时,△AEF的面积是( )| A、8 | B、16 | C、24 | D、32 |
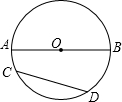 如图,AB是⊙O的直径,CD的是⊙O中非直径的任意一条弦,试比较AB与CD的大小,并说明理由.
如图,AB是⊙O的直径,CD的是⊙O中非直径的任意一条弦,试比较AB与CD的大小,并说明理由.