题目内容
已知一个二次函数的图象经过(-1,10),(1,4),(2,7)三点.求这个二次函数的解析式,并求出它的开口方向、对称轴和顶点坐标.
考点:待定系数法求二次函数解析式
专题:
分析:设二次函数的解析式为y=ax2+bx+c,把(-1,10),(1,4),(2,7)三点坐标代入,列方程组求a、b、c的值,确定函数解析式,根据二次函数解析式可知抛物线的对称轴及顶点坐标.
解答:解:设二次函数的解析式为y=ax2+bx+c,把(-1,10),(1,4),(2,7)各点代入上式得
,
解得
.
则抛物线解析式为y=2x2-3x+5;
由y=2x2-3x+5=2(x-
)+
可知,抛物线对称轴为直线x=
,顶点坐标为(
,
).
|
解得
|
则抛物线解析式为y=2x2-3x+5;
由y=2x2-3x+5=2(x-
| 3 |
| 4 |
| 31 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 31 |
| 8 |
点评:本题考查了用待定系数法求二次函数解析式的方法.关键是根据条件确定抛物线解析式的形式,再求其中的待定系数.一般式:y=ax2+bx+c(a≠0);顶点式y=a(x-h)2+k,其中顶点坐标为(h,k);交点式y=a(x-x1)(x-x2),抛物线与x轴两交点为(x1,0),(x2,0).

练习册系列答案
相关题目
在数|-4.5|,-|+2.1|,-(-0.8),+|-0|中,负数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
等腰三角形的一个内角是75°,它的顶角是( )
| A、30° | B、75° |
| C、30°或75° | D、105° |
下列计算正确的是( )
| A、-3+(-3)=0 | ||||
B、(-
| ||||
| C、-5×0=-5 | ||||
D、(-1
|
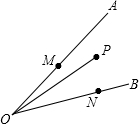 如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是
如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是