题目内容
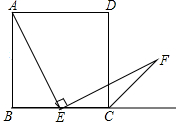 如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )A、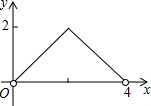 |
B、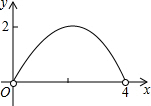 |
C、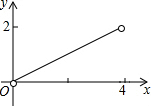 |
D、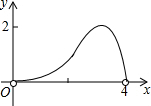 |
考点:动点问题的函数图象
专题:
分析:过E作EH⊥BC于H,求出EH=CH,求出△BAP∽△HPE,得出
=
,求出EH=x,代入y=
×CP×EH求出解析式,根据解析式确定图象即可.
| AB |
| PH |
| BP |
| EH |
| 1 |
| 2 |
解答:解: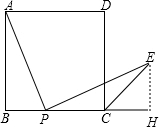 过E作EH⊥BC于H,
过E作EH⊥BC于H,
∵四边形ABCD是正方形,
∴∠DCH=90°,
∵CE平分∠DCH,
∴∠ECH=
∠DCH=45°,
∵∠H=90°,
∴∠ECH=∠CEH=45°,
∴EH=CH,
∵四边形ABCD是正方形,AP⊥EP,
∴∠B=∠H=∠APE=90°,
∴∠BAP+∠APB=90°,∠APB+∠EPH=90°,
∴∠BAP=∠EPH,
∵∠B=∠H=90°,
∴△BAP∽△HPE,
∴
=
,
∴
=
,
∴EH=x,
∴y=
×CP×EH
=
(4-x)•x
y=2x-
x2,
故选C.
 过E作EH⊥BC于H,
过E作EH⊥BC于H,∵四边形ABCD是正方形,
∴∠DCH=90°,
∵CE平分∠DCH,
∴∠ECH=
| 1 |
| 2 |
∵∠H=90°,
∴∠ECH=∠CEH=45°,
∴EH=CH,
∵四边形ABCD是正方形,AP⊥EP,
∴∠B=∠H=∠APE=90°,
∴∠BAP+∠APB=90°,∠APB+∠EPH=90°,
∴∠BAP=∠EPH,
∵∠B=∠H=90°,
∴△BAP∽△HPE,
∴
| AB |
| PH |
| BP |
| EH |
∴
| 4 |
| 4-x+EH |
| x |
| EH |
∴EH=x,
∴y=
| 1 |
| 2 |
=
| 1 |
| 2 |
y=2x-
| 1 |
| 2 |
故选C.
点评:本题考查了动点问题的函数图象,正方形性质,角平分线定义,相似三角形的性质和判定的应用,关键是能用x的代数式把CP和EH的值表示出来.

练习册系列答案
相关题目
已知反比例函数和正比例函数在第一象限的交点为A(1,3),则在第三象限的交点B为( )
| A、(-1,-3) |
| B、(-3,-1) |
| C、(-2,-6) |
| D、(-6,-2) |
反比例函数y=
图象上有三个点(-3,y1),(-1,y2),(2.y3),则y1,y2,y3的大小关系是( )
| 6 |
| x |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y3<y2<y1 |
 如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,∠DEB=90°,BC=10cm,AC=6cm,AB=5cm,则△BDE的周长为
如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,∠DEB=90°,BC=10cm,AC=6cm,AB=5cm,则△BDE的周长为
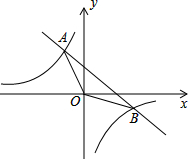 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数