题目内容
4.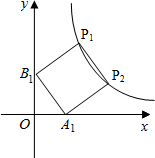 如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).
如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).
分析 作P1C⊥y轴于C,P2D⊥x轴于D,设P1(a,$\frac{2}{a}$),则CP1=a,OC=$\frac{2}{a}$,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D=$\frac{2}{a}$-a,则P2的坐标为($\frac{2}{a}$,$\frac{2}{a}$-a),然后把P2的坐标代入反比例函数y=$\frac{2}{x}$,得到a的方程,解方程求出a,得到P2的坐标.
解答  解:作P1C⊥y轴于C,P2D⊥x轴于D,如图,
解:作P1C⊥y轴于C,P2D⊥x轴于D,如图,
设P1(a,$\frac{2}{a}$),则CP1=a,OC=$\frac{2}{a}$,
∵四边形A1B1P1P2为正方形,
∴Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,
∴OB1=P1C=A1D=a,
∴OA1=B1C=P2D=$\frac{2}{a}$-a,
∴OD=a+$\frac{2}{a}$-a=$\frac{2}{a}$,
∴P2的坐标为($\frac{2}{a}$,$\frac{2}{a}$-a),
把P2的坐标代入y=$\frac{2}{x}$(x>0),得到($\frac{2}{a}$-a)•$\frac{2}{a}$=2,解得a=-1(舍)或a=1,
∴P2(2,1),
故答案为:(2,1).
点评 本题考查了反比例函数图象上点的坐标特点,也考查了正方形的性质和三角形全等的判定与性质以及解分式方程的方法,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
12. 如图,直线AB和CD相交于点O,∠AOD+∠BOC=200°,则∠AOC的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=200°,则∠AOC的度数为( )
 如图,直线AB和CD相交于点O,∠AOD+∠BOC=200°,则∠AOC的度数为( )
如图,直线AB和CD相交于点O,∠AOD+∠BOC=200°,则∠AOC的度数为( )| A. | 120° | B. | 100° | C. | 90° | D. | 80° |
19.如图1,E为矩形ABCD边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C时停止,点Q从点B出发沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )


| A. | 当t=11s时,y=40cm2 | B. | BE=10cm | ||
| C. | 当0≤t≤10时,y=$\frac{2}{5}$t2 | D. | 当t=16s时,∠PBQ=30° |
6.大家知道:“距离地面越远,温度越低”.小明查阅资料得到下面表格中的对应数据:
根据表中,请你帮助小明解决下列问题:
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为T=20-6h.
(2)当h=10km时,高空的温度T是多少?
(3)当T=-28℃时,距离地面的高度h是多少?
| 距离地面高度h/km | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 温度T/℃ | 20 | 14 | 8 | 2 | -4 | -10 | … |
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为T=20-6h.
(2)当h=10km时,高空的温度T是多少?
(3)当T=-28℃时,距离地面的高度h是多少?
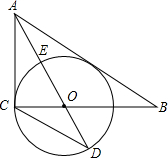 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O. 如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,AC为对角线,BM⊥AC于点M,交AD于点N,点O是BC边上一点,$\frac{OC}{BC}=\frac{1}{3}$,连接DO交AC于点P,OF⊥OD交BN于点E,交AB边于点F.
如图,在矩形ABCD中,$\frac{AB}{BC}=\frac{3}{5}$,AC为对角线,BM⊥AC于点M,交AD于点N,点O是BC边上一点,$\frac{OC}{BC}=\frac{1}{3}$,连接DO交AC于点P,OF⊥OD交BN于点E,交AB边于点F.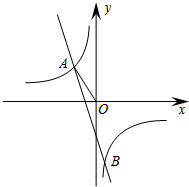 已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.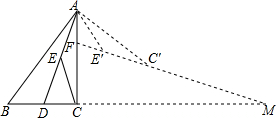 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.