题目内容
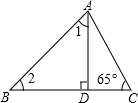如图，AD是△ABC边BC上的高，∠1=∠2，∠C=65°．求∠BAC的度数．考点：三角形内角和定理
专题：
分析：先根据AD⊥BC可知∠ADB=∠ADC=90°，再根据直角三角形的性质求出∠1与∠DAC的度数，由∠BAC=∠1+∠DAC即可得出结论．
解答：解：∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∴∠DAC=90°-65°=25°，∠1=∠2=45°，
∴∠BAC=∠1+∠DAC=45°+25°=70°．
∴∠ADB=∠ADC=90°，
∴∠DAC=90°-65°=25°，∠1=∠2=45°，
∴∠BAC=∠1+∠DAC=45°+25°=70°．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知：如图，△ABC中，BD是角平分线，AE是高，∠C=50°，∠BAE=30°，求：∠BDA的度数．
有理数a、b在数轴上位置如图所示，试化简|1-3b|+2|2+b|-|3b-2|．
如图，已知抛物线y=x2+bx+c与x轴交于点A，B，AB=2，与y轴交于点C，对称轴为直线x=2．