题目内容
9.化简:$\frac{x-y}{x-2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$的结果是$\frac{x-2y}{x+y}$.分析 首先将分子与分母能分解因式的进行分解因式进而约分求出即可.
解答 解:原式=$\frac{x-y}{x-2y}$×$\frac{(x-2y)^{2}}{(x-y)(x+y)}$=$\frac{x-2y}{x+y}$.
故答案为:$\frac{x-2y}{x+y}$.
点评 此题主要考查了分式的乘除运算,正确分解因式是解题关键.

练习册系列答案
相关题目
19.已知∠A是锐角,且sinA=$\frac{3}{5}$,则tanA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
1.下列从左边到右边的变形,是因式分解的是( )
| A. | 12a2b=3a•4ab | B. | (x+3)(x-3)=x2-9 | ||
| C. | 4x2+8x-1=4x(x+2)-1 | D. | x2+3x-4=(x-1)(x+4) |
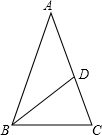 如图,△ABC中,AB=AC=1,∠ABC的平分线交AC于D,若∠A=36°,则cosA等于$\frac{\sqrt{5}+1}{4}$.
如图,△ABC中,AB=AC=1,∠ABC的平分线交AC于D,若∠A=36°,则cosA等于$\frac{\sqrt{5}+1}{4}$.