题目内容
4.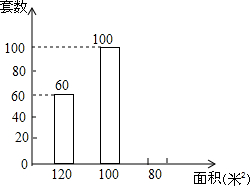 某房地产开发商开发了套内面积分别为“120米2”、“100米2”、“80米2”三种房源其200套,售房部将每种房源套数及每平方的价格绘制了表格和直方图如下:
某房地产开发商开发了套内面积分别为“120米2”、“100米2”、“80米2”三种房源其200套,售房部将每种房源套数及每平方的价格绘制了表格和直方图如下:| 房源类型 | 套内售价(元/米2) |
| 120米2 | 10000 |
| 100米2 | 8000 |
| 80米2 | 4750 |
(2)求每平方米售价的均价和众数(取整数);
(3)不同面积的三种房子都分别设计为甲、乙、丙三种户型,由于该房子所处地段好,质量又好,物业管理全国一流,所以购房者十分踊跃,几乎呈疯抢状态.但购房者都看好甲种户型,售房部为了将各种户型的房子都尽快卖出去,设计了一种规则:一个暗箱里放有标有1,2,3,4数字的四个形状大小完全一样的小球,另一个暗箱里放有标有-2,-1,1数字的三个形状大小完全一样的小球,购房者分别从两个箱子中各摸一个小球记下数字后放回各自的箱子中,若数字之和为2时选甲户型;若数字之和为1时选乙户型,若数字之和为0时选丙户型,请用列表或树状图求某购房者选购“120平方米”房子时选中甲种户型的概率.
分析 (1)首先设“80米2”的房子每平方米售价为x元,由题意可求得:80×40x=$\frac{1}{11}$(120×60×10000+100×100×8000+80×40x),继而求得答案;
(2)由题意可得每平方米售价的均价:$\frac{60×120×10000+100×100×8000+80×40×4750}{120×60+100×100+80×40}$,众数为:8000元/米2;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与数字之和为2情况,再利用概率公式即可求得答案.
解答  解:(1)200-100-60=40(套),
解:(1)200-100-60=40(套),
设“80米2”的房子每平方米售价为x元,
根据题意得:80×40x=$\frac{1}{11}$(120×60×10000+100×100×8000+80×40x),
解得:x=4750,
故答案为:4750.
(2)每平方米售价的均价:$\frac{60×120×10000+100×100×8000+80×40×4750}{120×60+100×100+80×40}$≈8196(元/米2);
众数为:8000元/米2.
(3)画树状图得:
∵共有12种等可能的结果,数字之和为2的有3种情况,
∴某购房者选购“120平方米”房子时选中甲种户型的概率为:$\frac{3}{12}$=$\frac{1}{4}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.如果3x2n-1ym与5my3是同类项,则m和n的取值是( )
| A. | 3和-2 | B. | -3和2 | C. | 3和2 | D. | -3和-2 |
12.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
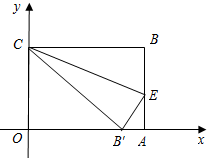 已知如图,在直角坐标系中放入一个边长OA为8的长方形纸片ABCO.
已知如图,在直角坐标系中放入一个边长OA为8的长方形纸片ABCO.