题目内容
14.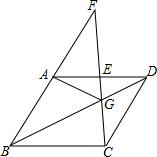 已知,菱形ABCD中,点G是对角线BD上一点,CG交BA的延长线于点F,求证:AG2=GE•GF.
已知,菱形ABCD中,点G是对角线BD上一点,CG交BA的延长线于点F,求证:AG2=GE•GF.
分析 根据菱形的性质得到AB∥CD,AD=CD,∠ADB=∠CDB,推出△ADG≌△CDG,得到∠EAG=∠DCG,等量代换得到∠EAG=∠F,求得△AEG∽△FGA,即可得到结论.
解答 解:∵四边形ABCD是菱形,
∴AB∥CD,AD=CD,∠ADB=∠CDB,
∴∠F∠FCD,
在△ADG与△CDG中,$\left\{\begin{array}{l}{AD=CD}\\{∠ADG=∠CDG}\\{DG=DG}\end{array}\right.$,
∴△ADG≌△CDG,
∴∠EAG=∠DCG,
∴∠EAG=∠F,
∵∠AGE=∠AGE,
∴△AEG∽△FGA,
∴$\frac{AG}{FG}=\frac{GE}{AG}$,
∴AG2=GE•GF.
点评 本题考查了相似三角形的判定和性质,菱形的性质,全等三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
5.既不是正数,也不是负数的数是( )
| A. | 1 | B. | 0 | C. | π | D. | $\frac{1}{3}$ |
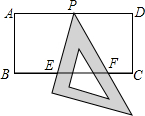 如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )
如图,在矩形ABCD中,AD=2,AB=1,P是AD的中点,等腰直角三角板45°角的顶点与点P重合,当此三角板绕点P旋转时,它的直角边和斜边所在的直线与BC分别相交于E、F两点.设线段BF=x,CE=y,则下列图象中,能表示y与x的函数关系的大致图象是( )
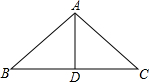 如图所示是一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,则$\frac{BD}{AB}$=$\frac{4}{5}$,$\frac{AD}{AB}$=$\frac{3}{5}$.
如图所示是一个等腰三角形形状的梁架,腰AB=5米,底边BC=8米,AD是底边BC上的高,则$\frac{BD}{AB}$=$\frac{4}{5}$,$\frac{AD}{AB}$=$\frac{3}{5}$.