题目内容
圆的面积s与半径r之间的关系式为S=πr2 , 其中常量是________ ,变量是________
 π S和r
【解析】常量就是在变化过程中不变的量,变量是指在变化过程中随时可以发生变化的量.由此可得,圆的面积s与半径r之间的关系式为S=πr2 ,常量是π,变量是S和r.
π S和r
【解析】常量就是在变化过程中不变的量,变量是指在变化过程中随时可以发生变化的量.由此可得,圆的面积s与半径r之间的关系式为S=πr2 ,常量是π,变量是S和r.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
先化简,再求值:-(a2-2ab)·9a2-(9ab3+12a4b2)÷3ab,其中a=-1,b=2.
 -49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49.
-49
【解析】试题分析:利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后,合并同类项化为最简,再代入求值即可.
试题解析:
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
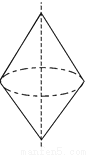
将a=-1,b=2代入得,原式=-49. 选择将三角形绕直线l旋转一周,可以得到如图所示主体图形的是( )
A. 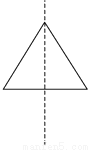 B.
B. 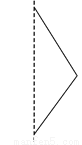 C.
C. 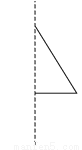 D.
D. 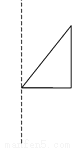
 B
【解析】解:A、C旋转一周后只有一个圆锥,B旋转后有上下两个同底的圆锥,D旋转后是一个圆柱去掉一个圆锥.故选B.
B
【解析】解:A、C旋转一周后只有一个圆锥,B旋转后有上下两个同底的圆锥,D旋转后是一个圆柱去掉一个圆锥.故选B. 两条直线平行,同旁内角相等。 (___)
 ×
【解析】试题分析:两条平行线被第三条直线所截,所形成的同旁内角互补,故本题的答案为“×”.
×
【解析】试题分析:两条平行线被第三条直线所截,所形成的同旁内角互补,故本题的答案为“×”. 已知函数y= x3+2,不画图象,解答下列问题:
x3+2,不画图象,解答下列问题:
(1)判断A(0,2)、B(2,0)、C(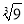 , ﹣1)三点是否在该函数图象上,说明理由;
, ﹣1)三点是否在该函数图象上,说明理由;
(2)若点P(a,0)、Q(﹣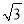 , b)都在该函数的图象上,试求a、b的值.
, b)都在该函数的图象上,试求a、b的值.
 (1) B,C点不在该函数图象上,A点在该函数图象上;(2) a=,b=
【解析】试题分析:(1)分别将A,B,C点代入函数关系式进而判断即可;(2)分别将P,Q点代入函数关系式进而得出答案.
试题解析:
(1)当x=0时,y=2,
当x=2时,y=+2=,
当x=时,y=5,
故B,C点不在该函数图象上,A点在该函数图象上;
(2)当y=0时,0=x3+...
(1) B,C点不在该函数图象上,A点在该函数图象上;(2) a=,b=
【解析】试题分析:(1)分别将A,B,C点代入函数关系式进而判断即可;(2)分别将P,Q点代入函数关系式进而得出答案.
试题解析:
(1)当x=0时,y=2,
当x=2时,y=+2=,
当x=时,y=5,
故B,C点不在该函数图象上,A点在该函数图象上;
(2)当y=0时,0=x3+... 如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
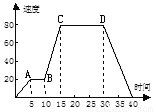
(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.
A. 1个 B. 2个 C. 3个 D. 4个
 C
【解析】试题分析:仔细分析图象特征,根据横轴和纵轴的意义依次分析各小题即可作出判断.
【解析】
由图可得,在x=40时,速度为0,故(1)(3)正确;
AB段,y的值相等,故速度不变,故(2)正确;
x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(4)错误;
故选C.
C
【解析】试题分析:仔细分析图象特征,根据横轴和纵轴的意义依次分析各小题即可作出判断.
【解析】
由图可得,在x=40时,速度为0,故(1)(3)正确;
AB段,y的值相等,故速度不变,故(2)正确;
x=30时,y=80,即在第30分钟时,汽车的速度是80千米/时;故(4)错误;
故选C. 被誉为“沙漠之舟”的骆驼,其体温随着气温的变化而变化.在这个问题中,自变量是( )
A. 骆驼 B. 沙漠 C. 气温 D. 体温
 C
【解析】由于体温随着气温的变化而变化,则自变量是气温,因变量是体温.
故选:C.
C
【解析】由于体温随着气温的变化而变化,则自变量是气温,因变量是体温.
故选:C. 直角坐标系中,已知点P(-2,-1),点T(t,0)是x轴上的一个动点.

(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时,△P′TO是等腰三角形?
 (1)点P关于原点的对称点P′的坐标为(2,1);(2)综上所述,符合条件的t的值为-, , ,4.
【解析】试题分析: (1)根据坐标关于原点对称的特点即可得出点P′的坐标,(2)要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原...
(1)点P关于原点的对称点P′的坐标为(2,1);(2)综上所述,符合条件的t的值为-, , ,4.
【解析】试题分析: (1)根据坐标关于原点对称的特点即可得出点P′的坐标,(2)要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原... 下面说法错误的是 ( )
A. 三角形的三条角平分线交于一点 B. 三角形的三条中线交于一点
C. 三角形的三条高交于一点 D. 三角形的三条高所在的直线交于一点
 C
【解析】A. 三角形的三条角平分线交于一点,是三角形的内心,故命题正确;
B. 三角形的三条中线交于一点,是三角形的重心,故命题正确;
三角形的三条高所在的直线交于一点,三条高不一定相交,故C错误,D正确。
故选C.
C
【解析】A. 三角形的三条角平分线交于一点,是三角形的内心,故命题正确;
B. 三角形的三条中线交于一点,是三角形的重心,故命题正确;
三角形的三条高所在的直线交于一点,三条高不一定相交,故C错误,D正确。
故选C. 
