题目内容
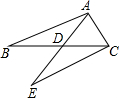如图所示，△ABC中，AC=5，中线AD=7，△EDC是由△ADB旋转180°所得，则AB边的取值范围是（ ）| A、1＜AB＜29 |
| B、4＜AB＜24 |
| C、5＜AB＜19 |
| D、9＜AB＜19 |
考点：旋转的性质
专题：
分析：根据旋转的性质可得DE=AD，AB=CE，再求出AE，然后根据三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出CE的取值范围，即为AB的取值范围．
解答：解：∵△EDC是由△ADB旋转180°所得，
∴DE=AD=7，AB=CE，
∴AE=AD+DE=7+7=14，
∵14-5=9，14+5=19，
∴由三角形的三边关系得，9＜CE＜19，
∴9＜AB＜19．
故选D．
∴DE=AD=7，AB=CE，
∴AE=AD+DE=7+7=14，
∵14-5=9，14+5=19，
∴由三角形的三边关系得，9＜CE＜19，
∴9＜AB＜19．
故选D．
点评：本题考查了旋转的性质，三角形的三边关系，熟记旋转的性质并求出边AE的长是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
在直角坐标系中，⊙P、⊙Q的位置如图所示．在⊙P上且在⊙Q内部的格点坐标是
如图，AC是正方形ABCD的对角线，AE平分∠BAC，EF⊥AC交AC于点F，若BE=2，则CF长为
在Rt△ABC中，∠ABC=90°，D为AC上一点，E是BD中点，∠1=∠2，求证：∠ADB=2∠ABD．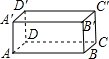
如图是一个放置雕塑的长方形底座，AB=12米，BC=2米，BB′=3米．一只蚂蚁从A点出发，以2厘米/秒的速度沿长方形表面爬到C′至少需要一个立体图形三视图如图所示，那么这个立体图形的名称是（ ）
| A、三棱柱 | B、四棱柱 |
| C、三棱锥 | D、四棱锥 |
