题目内容
7.解方程(1)2x2-3=-6x (配方法)
(2)4x2-3x-1=0(公式法)
分析 (1)利用配方法得到(x+$\frac{3}{2}$)2=$\frac{15}{4}$,然后再利用直接开平方法解方程;
(2)先计算判别式的值,然后根据求根公式解方程.
解答 解:(1)x2+3x=$\frac{3}{2}$,
x2+3x+$\frac{9}{4}$=$\frac{15}{4}$,
(x+$\frac{3}{2}$)2=$\frac{15}{4}$,
x+$\frac{3}{2}$=±$\frac{\sqrt{15}}{2}$,
所以x1=$\frac{-3+\sqrt{15}}{2}$,x2=$\frac{-3-\sqrt{15}}{2}$;
(1)∵a=4,b=-3,c=-1,
∴b2-4ac=(-3)2-4×4×(-1)=25>0,
∴x=$\frac{3±\sqrt{25}}{2×4}$=$\frac{3±5}{8}$,
∴x1=1,x2=-$\frac{1}{4}$.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.也考查了配方法解一元二次方程.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
18.某企业信息部进行市场调查发现:
信息一、如果单独投资A种产品,所投资利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获利润3.2万元.
(1)从所学过的函数中猜想yA与x之间的关系,并求出yA与x的函数关系式;
(2)求出yB与x的函数关系式,并求想利润yB为3(万元)应投资金额;
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
信息一、如果单独投资A种产品,所投资利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
| x(万元) | 1 | 2 | 2.5 | 3 | 5 |
| yA(万元) | 0.4 | 0.8 | 1 | 1.2 | 2 |
(1)从所学过的函数中猜想yA与x之间的关系,并求出yA与x的函数关系式;
(2)求出yB与x的函数关系式,并求想利润yB为3(万元)应投资金额;
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
16.把抛物线y=2x2向左平移2个单位,再向上平移1个单位,所得到的抛物线的解析式为( )
| A. | y=2(x+2)2+1 | B. | y=2(x+2)2-1 | C. | y=2(x-2)2-1 | D. | y=2(x-2)2+1 |
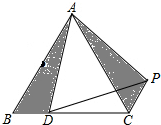 如图,△ABC为等边三角形,D为BC边上一点,△ABD经过逆时针旋转后得到△ACP,则
如图,△ABC为等边三角形,D为BC边上一点,△ABD经过逆时针旋转后得到△ACP,则 如图,△ABC中,BA=BC,∠ABC=40°,∠ABC的平分线与BC的垂直平分线交于点O,E在BC边上,F在AC边上,将∠A沿直线EF翻折,使点A与点O恰好重合,则∠OEF的度数是70°.
如图,△ABC中,BA=BC,∠ABC=40°,∠ABC的平分线与BC的垂直平分线交于点O,E在BC边上,F在AC边上,将∠A沿直线EF翻折,使点A与点O恰好重合,则∠OEF的度数是70°.