题目内容
2．对于抛物线y=（x-1）2-2的图象，下列说法正确的是（ ）| A． | 开口向下 | B． | 对称轴是直线x=-1 | ||
| C． | 顶点坐标是（1，2） | D． | 与x轴有两个交点 |
分析 根据二次函数的性质对各开口方向、顶点坐标、对称轴以及与x轴的交点坐标进行判断即可．
解答 解：抛物线y=（x-1）2-2的图象，开口向上，对称轴是直线x=1，顶点坐标是（1，-2），b2-4ac=8＞0，与x轴有两个交点．
故选：D．
点评 本题考查了二次函数的性质，掌握利用顶点式求抛物线的开口方向、顶点坐标、对称轴与最值是解决问题的关键．
练习册系列答案
巧学巧练系列答案
课课练江苏系列答案
相关题目
13．
如图，数轴上表示$\sqrt{3}$，2的对应点分别为A、B，点B关于点A的对称点为C，则点C表示的实数为（ ）
如图，数轴上表示$\sqrt{3}$，2的对应点分别为A、B，点B关于点A的对称点为C，则点C表示的实数为（ ）| A． | $\sqrt{3}$-2 | B． | 2-$\sqrt{3}$ | C． | $\sqrt{3}$-1 | D． | $2\sqrt{3}$-2 |
7．抛物线y=-2x2向左平移5个单位长度，然后向上平移3个单位长度，则平移后抛物线的解析式为（ ）
| A． | y=-2（x-5）2-3 | B． | y=-2（x+5）2-3 | C． | y=-2（x-5）2+3 | D． | y=-2（x+5）2+3 |
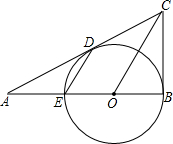如图，已知，BE是⊙O的直径，BC切⊙O于B，弦DE∥OC，连接CD并延长交BE的延长线于点A．
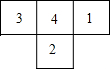一个几何体由几个大小形状相同的小立方块搭成，从上面观察这个几何体，看到的形状如图所示，其中小立方块中的数字表示在该位置的小立方块的个数，请画出从正面、左面看到的这个几何体的形状．