题目内容
 如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题:(1)判断△ABC的形状,并说明理由.
(2)作出△ABC关于点(0,1)成中心对称的△A1B1C1;并写出△ABC内的任意一点M(a,b)关于点(0,1)的对称点M1的坐标是
考点:作图-旋转变换,坐标与图形变化-旋转
专题:
分析:(1)可利用勾股定理以及勾股定理的逆定理得出△ABC是等腰直角三角形;
(2)根据A,B,C对应点坐标的变化得出规律,进而得出M1的坐标.
(2)根据A,B,C对应点坐标的变化得出规律,进而得出M1的坐标.
解答: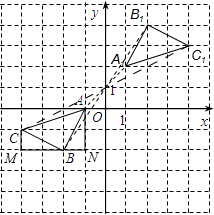 解:(1)△ABC是等腰直角三角形,
解:(1)△ABC是等腰直角三角形,
方法一:∵A(-1,0)、B(-2,-2)、C(-4,-1)
∴AB=BC=
,AC=
,
∴△ABC是等腰三角形,
∵AB2+BC2=AC2=10,
根据勾股定理逆定理,可知,∠ABC=90°,
∴△ABC是等腰直角三角形,
方法二:如图,∵在Rt△ANB和Rt△BMC中,
,
∴△MBC≌△NAB(HL),
∴BC=AB,∠ABN=∠BCM,
∴∠NBA+∠MBC=90°,
∴∠ABC=90°,
∴△ABC是等腰直角三角形;
(2)如图所示,∵A(-1,0),A1(1,2),B(-2,-2),B1(2,4),
∴点M(a,b)关于点(0,1)的对称点M1的坐标是:(-a,2-b).
 解:(1)△ABC是等腰直角三角形,
解:(1)△ABC是等腰直角三角形,方法一:∵A(-1,0)、B(-2,-2)、C(-4,-1)
∴AB=BC=
| 5 |
| 10 |
∴△ABC是等腰三角形,
∵AB2+BC2=AC2=10,
根据勾股定理逆定理,可知,∠ABC=90°,
∴△ABC是等腰直角三角形,
方法二:如图,∵在Rt△ANB和Rt△BMC中,
|
∴△MBC≌△NAB(HL),
∴BC=AB,∠ABN=∠BCM,
∴∠NBA+∠MBC=90°,
∴∠ABC=90°,
∴△ABC是等腰直角三角形;
(2)如图所示,∵A(-1,0),A1(1,2),B(-2,-2),B1(2,4),
∴点M(a,b)关于点(0,1)的对称点M1的坐标是:(-a,2-b).
点评:此题主要考查了勾股定理以及逆定理的应用,根据已知得出对应点坐标的性质是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
在2,-2,
,-
四个数中最小的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 (1)三角形外心是
(1)三角形外心是