题目内容
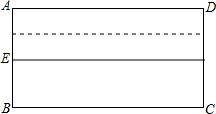在长方形纸片ABCD中，AB=1，BC=2，设E为边BC的中点，现将纸片折叠，使A、E重合，则折痕将长方形纸片分为两部分中，较大部分面积与较小部分面积之比为________．
3：1
分析：根据线段的中点的定义求出AE=BE=
，设折痕与AB的交点为F，根据折叠的性质求出AF，然后出BF，利用长方形的面积公式求出两个部分的面积，然后相比即可得解．
解答：
解：∵E为边BC的中点，
∴AE=BE=AB=，
设折痕与AB的交点为F，
由折叠的性质得，AF=EF=AE=×=
，
∴BF=+=
，
又∵BC=2，
∴较大部分面积为×2=
，
较小部分面积为×2=，
∴较大部分面积与较小部分面积之比为3：1．
故答案为：3：1．
点评：本题考查了翻折变换，长方形的性质，熟记各性质并求出被折痕分成的两个长方形的宽是解题的关键．
分析：根据线段的中点的定义求出AE=BE=
，设折痕与AB的交点为F，根据折叠的性质求出AF，然后出BF，利用长方形的面积公式求出两个部分的面积，然后相比即可得解．解答：
解：∵E为边BC的中点，∴AE=BE=
AB=，设折痕与AB的交点为F，
由折叠的性质得，AF=EF=
AE=×=，∴BF=
+=，又∵BC=2，
∴较大部分面积为
×2=，较小部分面积为
×2=，∴较大部分面积与较小部分面积之比为3：1．
故答案为：3：1．
点评：本题考查了翻折变换，长方形的性质，熟记各性质并求出被折痕分成的两个长方形的宽是解题的关键．
练习册系列答案
相关题目
在长方形纸片ABCD中，AD=6cm，AB=18cm，按如图方式折叠，使点B与点D重合，折痕为EF，则△ADE面积=
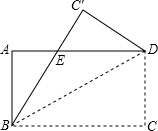如图，在长方形纸片ABCD中，四个内角均为直角，AB=CD，AD=BC，将长方形纸片ABCD沿对角线BD进行折叠，点C的对称点为C′，BC′交AD于点E．
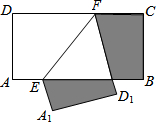如图，在长方形纸片ABCD中，AB=2，BC=1，点E、F分别在AB、CD上，将纸片沿EF折叠，使点A、D分别落在点A1、D1处，则阴影部分图形的周长为（ ）
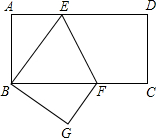如图，在长方形纸片ABCD中，AD=8cm，AB=4cm沿EF折叠使点B与点D重合，点C落在点G处．