题目内容
 在长方形纸片ABCD中,AD=6cm,AB=18cm,按如图方式折叠,使点B与点D重合,折痕为EF,则△ADE面积=
在长方形纸片ABCD中,AD=6cm,AB=18cm,按如图方式折叠,使点B与点D重合,折痕为EF,则△ADE面积=分析:因为B与点D重合,所以AE+DE=AB,设AE=x,再根据勾股定理可求出x的值,再由直角三角形的面积公式求解即可.
解答:解:设AE=x,则BE=18-x,
∵图形折叠后点B与点D重合,
∴DE=BE=18-x,
∵△ADE是直角三角形,
∴DE2=AE2+AD2,即(18-x)2=x2+62,
解得x=8,
∴S△ADE=
AE•AD=
×8×6=24cm2.
故答案为:24.
∵图形折叠后点B与点D重合,
∴DE=BE=18-x,
∵△ADE是直角三角形,
∴DE2=AE2+AD2,即(18-x)2=x2+62,
解得x=8,
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:24.
点评:本题考查的是图形翻折变换的性质及直角三角形的面积、勾股定理,解答此题的关键是熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目

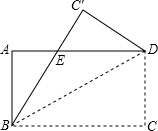 如图,在长方形纸片ABCD中,四个内角均为直角,AB=CD,AD=BC,将长方形纸片ABCD沿对角线BD进行折叠,点C的对称点为C′,BC′交AD于点E.
如图,在长方形纸片ABCD中,四个内角均为直角,AB=CD,AD=BC,将长方形纸片ABCD沿对角线BD进行折叠,点C的对称点为C′,BC′交AD于点E.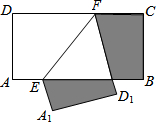 如图,在长方形纸片ABCD中,AB=2,BC=1,点E、F分别在AB、CD上,将纸片沿EF折叠,使点A、D分别落在点A1、D1处,则阴影部分图形的周长为( )
如图,在长方形纸片ABCD中,AB=2,BC=1,点E、F分别在AB、CD上,将纸片沿EF折叠,使点A、D分别落在点A1、D1处,则阴影部分图形的周长为( )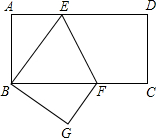 如图,在长方形纸片ABCD中,AD=8cm,AB=4cm沿EF折叠使点B与点D重合,点C落在点G处.
如图,在长方形纸片ABCD中,AD=8cm,AB=4cm沿EF折叠使点B与点D重合,点C落在点G处.