题目内容
如图1,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
=n,其中0<n≤1.

(1)如图2,当n=1(即M点与D点重合),m=2时,则
=
;
(2)如图3,当n=
(M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(3)如图1,当m=2(AB=2AD),n的值发生变化时,
的值是否发生变化?说明理由.
| AM |
| AD |

(1)如图2,当n=1(即M点与D点重合),m=2时,则
| BE |
| AE |
| 5 |
| 3 |
| 5 |
| 3 |
(2)如图3,当n=
| 1 |
| 2 |
(3)如图1,当m=2(AB=2AD),n的值发生变化时,
| BE-CF |
| AM |
分析:(1)由条件可知,当n=1(即M点与D点重合),m=2时,AB=2AD,设AD=a,则AB=2a,由矩形的性质可以得出△ADE≌△NDF,就可以得出AE=NF,DE=DF,在Rt△AED中,由勾股定理就可以表示出AE的值,再求出BE的值就可以得出结论;
(2)延长PM交EA延长线于G,由条件可以得出△PDM≌△GAM,△EMP≌△EMG由全等三角形的性质就可以得出结论;
(3)如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,通过证明△ABM∽△KFE,就可以得出
=
即
=
,由AB=2AD=2BC,BK=CF就可以得出
的值是
为定值.
(2)延长PM交EA延长线于G,由条件可以得出△PDM≌△GAM,△EMP≌△EMG由全等三角形的性质就可以得出结论;
(3)如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,通过证明△ABM∽△KFE,就可以得出
| EK |
| AM |
| KF |
| AB |
| BE-BK |
| AM |
| BC |
| AB |
| BE-CF |
| AM |
| 1 |
| 2 |
解答:解:(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°.
∵AB=mAD,且n=2,
∴AB=2AD.
∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,
∴∠ADE=∠NDF.
在△ADE和△NDF中,
,
∴△ADE≌△NDF(ASA),
∴AE=NF,DE=DF.
∵FN=FC,
∴AE=FC.
∵AB=CD,
∴AB-AE=CD-CF,
∴BE=DF,
∴BE=DE.
Rt△AED中,由勾股定理,得
AE2=DE2-AD2,
AE2=(2AD-AE)2-AD2,
∴AE=
AD,
∴BE=2AD-
AD=
AD.
∴
=
=
.
(2)如图3,延长PM交EA延长线于G,
∴∠GAM=90°.
∵M为AD的中点,
∴AM=DM.
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,AB∥CD,
∴∠GAM=∠PDM.
在△GAM和△PDM中,
,
∴△GAM≌△PDM(ASA),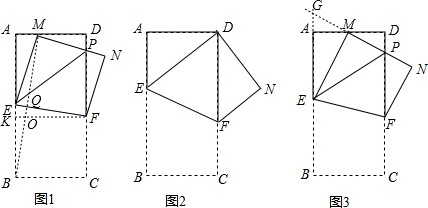
∴MG=MP,
在△EMP和△EMG中,
,
∴△EMP≌△EMG(SAS),
∴EG=EP,
∴AG+AE=EP,
∴PD+AE=EP,
即EP=AE+DP;
(3)
=
的值不变,
理由:如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,
∵EM=EB,∠MEF=∠BEF,
∴EF⊥MB,
即∠FQO=90°,
∵四边形FKBC是矩形,
∴KF=BC,FC=KB,
∵∠FKB=90°,
∴∠KBO+∠KOB=90°,
∵∠QOF+∠QFO=90°,∠QOF=∠KOB,
∴∠KBO=∠OFQ,
∵∠A=∠EKF=90°,
∴△ABM∽△KFE,
∴
=
即
=
,
∵AB=2AD=2BC,BK=CF,
∴
=
,
∴
的值不变.
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°.
∵AB=mAD,且n=2,
∴AB=2AD.
∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,
∴∠ADE=∠NDF.
在△ADE和△NDF中,
|
∴△ADE≌△NDF(ASA),
∴AE=NF,DE=DF.
∵FN=FC,
∴AE=FC.
∵AB=CD,
∴AB-AE=CD-CF,
∴BE=DF,
∴BE=DE.
Rt△AED中,由勾股定理,得
AE2=DE2-AD2,
AE2=(2AD-AE)2-AD2,
∴AE=
| 3 |
| 4 |
∴BE=2AD-
| 3 |
| 4 |
| 5 |
| 4 |
∴
| BE |
| AE |
| ||
|
| 5 |
| 3 |
(2)如图3,延长PM交EA延长线于G,
∴∠GAM=90°.
∵M为AD的中点,
∴AM=DM.
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,AB∥CD,
∴∠GAM=∠PDM.
在△GAM和△PDM中,
|
∴△GAM≌△PDM(ASA),

∴MG=MP,
在△EMP和△EMG中,
|
∴△EMP≌△EMG(SAS),
∴EG=EP,
∴AG+AE=EP,
∴PD+AE=EP,
即EP=AE+DP;
(3)
| BE-CF |
| AM |
| 1 |
| 2 |
理由:如图1,连接BM交EF于点Q,过点F作FK⊥AB于点K,交BM于点O,
∵EM=EB,∠MEF=∠BEF,
∴EF⊥MB,
即∠FQO=90°,
∵四边形FKBC是矩形,
∴KF=BC,FC=KB,
∵∠FKB=90°,
∴∠KBO+∠KOB=90°,
∵∠QOF+∠QFO=90°,∠QOF=∠KOB,
∴∠KBO=∠OFQ,
∵∠A=∠EKF=90°,
∴△ABM∽△KFE,
∴
| EK |
| AM |
| KF |
| AB |
| BE-BK |
| AM |
| BC |
| AB |
∵AB=2AD=2BC,BK=CF,
∴
| BE-CF |
| AM |
| 1 |
| 2 |
∴
| BE-CF |
| AM |
点评:本题是一道相似性的综合试题,考查了相似三角形的判定与性质、折叠的性质、全等三角形的判定与性质、矩形的性质以及等腰三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 20、如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′等于
20、如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′等于
 8、如图所示,长方形纸片ABCD,BC=12,点M在BC上,将纸片沿EF折叠,使点D落在点M处,若AE=2,则EM的长为
8、如图所示,长方形纸片ABCD,BC=12,点M在BC上,将纸片沿EF折叠,使点D落在点M处,若AE=2,则EM的长为 如图,把一长方形纸片ABCD沿EG折叠后,点A、B分别落在A′、B′的位置上,EA′与BC相交于点F,已知∠1=130°,则∠2的度数是( )
如图,把一长方形纸片ABCD沿EG折叠后,点A、B分别落在A′、B′的位置上,EA′与BC相交于点F,已知∠1=130°,则∠2的度数是( ) =n,其中0<n≤1.
=n,其中0<n≤1.
 =______;
=______; (M为AD的中点),m的值发生变化时,求证:EP=AE+DP;
(M为AD的中点),m的值发生变化时,求证:EP=AE+DP; 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.