题目内容
12.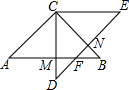 如图,△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,将△ABC绕着点C逆时针旋转45°后得到△DEC,AB、DE交于点F,CD交AB于M,CB交DE于N.
如图,△ABC中,∠ACB=90°,AC=BC=2$\sqrt{2}$,将△ABC绕着点C逆时针旋转45°后得到△DEC,AB、DE交于点F,CD交AB于M,CB交DE于N.(1)求证:四边形AFEC是菱形;
(2)求四边形CMFN的面积.
分析 (1)先证明四边形ACEF是平行四边形,再利用邻边相等证明是菱形即可.
(2)根据S四边形CMFN=S△CBM-S△BNF即可计算.
解答  (1)证明:∵AB=BC,∠ACB=90°,
(1)证明:∵AB=BC,∠ACB=90°,
∴∠A=∠B=∠D=∠E=45°,
∵∠ACD=∠ECB=45°,
∴∠AMC=∠CNE=90°,
∴∠ACB=∠FNB=90°,
∴AC∥ED,
∵∠ECB=∠B=45°,
∴CE∥AB,
∴四边形ACEF是平行四边形,
∵CA=CE,
∴四边形ACEF是菱形.
(2)解:∵AC=CB=2$\sqrt{2}$,CM⊥AB,∠ACB=90°,
∴CM=2,同理CN=2,BN=FN=2$\sqrt{2}$-2
∴S四边形CMFN=S△CBM-S△BNF=$\frac{1}{2}$×22-$\frac{1}{2}$×(2$\sqrt{2}$-2)2=8$\sqrt{2}$-10.
点评 本题考查旋转变换、菱形的判定和性质等知识.解图的关键是熟练掌握菱形的判定方法以及性质,学会利用分割法求四边形面积,属于中考常考题型.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
3.下列“表情图”中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.蚕丝是最细的天然纤维,它的截面直径约为0.000001米,这一数据用科学记数法表示为( )
| A. | 1×106米 | B. | 1×10-5米 | C. | 1×10-6米 | D. | 1×105米 |
4.下列几组数中,是勾股数的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 15,8,17 | C. | 13,14,15 | D. | $\frac{3}{5}$,$\frac{4}{5}$,1 |
7. 如图,将要给甲、乙、丙三户接电表,若使每相邻两户的电线等距排列,则三户所用的电线( )
如图,将要给甲、乙、丙三户接电表,若使每相邻两户的电线等距排列,则三户所用的电线( )
 如图,将要给甲、乙、丙三户接电表,若使每相邻两户的电线等距排列,则三户所用的电线( )
如图,将要给甲、乙、丙三户接电表,若使每相邻两户的电线等距排列,则三户所用的电线( )| A. | 甲户最长 | B. | 乙户最长 | C. | 丙户最长 | D. | 三户一样长 |
 如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是5$\sqrt{5}$.
如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是5$\sqrt{5}$. 如图,矩形ABCD的两邻边长分别为一元二次方程x2-7x+12=0的两个实数根,则矩形ABCD的面积为12.
如图,矩形ABCD的两邻边长分别为一元二次方程x2-7x+12=0的两个实数根,则矩形ABCD的面积为12.