题目内容
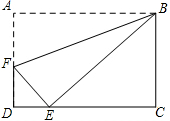 如图,在矩形ABCD中,AB:BC=2:
如图,在矩形ABCD中,AB:BC=2:| 3 |
(1)DE=EC;
(2)AF=2FD.
考点:翻折变换(折叠问题)
专题:
分析:(1)根据翻折变换的性质及勾股定理求出线段EC的长度问题即可解决.
(2)根据翻折变换的性质结合勾股定理求出AF的长度,进而求出DF的长度问题即可解决.
(2)根据翻折变换的性质结合勾股定理求出AF的长度,进而求出DF的长度问题即可解决.
解答: 解:(1)∵AB:BC=2:
解:(1)∵AB:BC=2:
,
∴可设AB=2k,则BC=
k
由题意得:
BE=AB=2k,
∵四边形ABCD为矩形,
∴∠C=90°,
由勾股定理得:
EC2=BE2-BC2=4k2-3k2=k2,
∴EC=k,DE=2k-k=k,
∴DE=EC.
(2)由题意得:
AF=EF(设为x),
则DF=
k-x,
由勾股定理得:
x2=(
k-x)2+k2,
解得:x=
=
∴DF=
k-
=
,
∴AF=2FD.
 解:(1)∵AB:BC=2:
解:(1)∵AB:BC=2:| 3 |
∴可设AB=2k,则BC=
| 3 |
由题意得:
BE=AB=2k,
∵四边形ABCD为矩形,
∴∠C=90°,
由勾股定理得:
EC2=BE2-BC2=4k2-3k2=k2,
∴EC=k,DE=2k-k=k,
∴DE=EC.
(2)由题意得:
AF=EF(设为x),
则DF=
| 3 |
由勾股定理得:
x2=(
| 3 |
解得:x=
| 2k | ||
|
2
| ||
| 3 |
∴DF=
| 3 |
| 2k | ||
|
| ||
| 3 |
∴AF=2FD.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质找出图中隐含的等量关系;根据勾股定理等几何知识来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,直线y=x+4与x轴、y轴分别交于A、B两点,直线y=-x+b过点B且与x轴交于点C.求直线BC的表达式.
如图,直线y=x+4与x轴、y轴分别交于A、B两点,直线y=-x+b过点B且与x轴交于点C.求直线BC的表达式. 如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.
如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算. 如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.
如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长. 如图,在△ABC中,∠A=30°,∠B-∠C=60°,BC=2,求AC的长.
如图,在△ABC中,∠A=30°,∠B-∠C=60°,BC=2,求AC的长. 如图,点A,B在数轴上,它们所对应的数分别是-5,
如图,点A,B在数轴上,它们所对应的数分别是-5, 如图所示,两条直线l1,l2的交点坐标可以看作方程组
如图所示,两条直线l1,l2的交点坐标可以看作方程组