Question

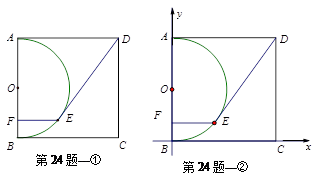
在边长为10的正方形ABCD中，以AB为直径作半圆O，如图①，E是半圆上一动点，过点E作EF⊥AB，垂足为F，连结DE.

（1）当DE=10时，求证：DE与圆O相切；

（2）求DE的最长距离和最短距离；

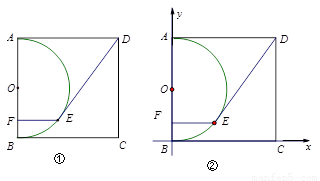
（3）如图②，建立平面直角坐标系，当DE =10时，试求直线DE的解析式.

 

Answer 1

【答案】

（1）证明见解析（2）（3）或

【解析】（1）证明：连结，

由题意得，------------1分

，，为公共边

∴ 

∴-------------------2分

（利用勾股定理逆定理相应给分）

∴

∴与圆相切.-------------------3分

 

（2）当点运动到与点重合的位置时，

为正方形的对角线，所以此时最长，有：

-----------------4分

当点运动到线段与半圆的交点处时，最短.

-----------------5分

证明如下：

在半圆上任取一个不与点重合的点，连结，.

在中，∵   即：，

∵    ∴

∵点是任意一个不与点重合的点，∴此时最短.        -----------------6分

∴-------------7分

 

（3）当点E与点A重合时，DE=DA=10，此时，直线DE的解析式为y=10；

---------8分

当点E与点A不重合时，过点E作GH ⊥轴，分别交，轴于点，，连结.

则四边形是矩形，且为圆的切线

∴=90°

∴-----------------------9分

又∵

∴∽

∴----------------------10分

设，则有：，

得：，-----------------------11分

解得：，  即：----------------12分

又直线DE过点D(10,10),设直线解析式为，则有：，

解得：，即：

∴当时，直线的解析式为或-----------------------14分

 

以下两种解法涉及高中知识，仅供参考：

另解2:

（1）当点E与点A重合时，DE=DA=10，此时，直线DE的解析式为y=10；

（2）当点E与点A不重合时，，

设直线且经过点（10，10），代入求得

所以直线DE的解析式为

 

另解3:

依题意得:点O的坐标为(0,5),设直线DE的解析式为

由点到直线的距离公式得: ,即    ①

直线DE过点D(10,10),得    ②

由①②解得：，解得

所以直线DE的解析式为

（1）如图1，连接OE，OD，由题意得，DE=DA=10，利用（SSS）判定△AOD≌△EOD，从可得∠OED=∠OAD=90°即可．

（2）当点E运动到与B点重合的位置时，如图2，DE为正方形ABCD的对角线，所以此时DE最长，利用勾股定理求得DE，证明当点E运动到线段OD与半圆O的交点处时，DE最短．然后求得DE=OD-OE即可．

（3）当点E与点A重合时，DE=DA=10，此时，直线DE的解析式为y=10；如图4，当点E与点A不重合时，过点E作GH⊥x轴，分别交AD，x轴于点G，H，连接OE．则四边形AFEG是矩形，且DE为圆O的切线，求证△OFE∽△DGE，利用其对应边成比例，设E（m，n），则有：EF=m，OF=OB-FB=5-n求得即可