题目内容
如图，在边长为10的正方形ABCD中，内接六个大小相同的正方形，P、Q、M、N是落在大正方形边上的顶点．则这六个小正方形的面积和是分析：如图，过点Q作QF⊥AD，垂足为F，可以得到△BQP∽△FQN，再根据相似三角形对应边成比例的性质列式求解即可得到QB和DN，根据勾股定理可求QN的长，从而求出六个小正方形的面积和．
解答：
解：如图所示：
∵正方形ABCD边长为10，
∴∠A=∠B=90°，AB=10，
过点Q作QF⊥AD，垂足为F，则∠4=∠5=90°，
∴四边形AFQB是矩形，
∴∠2+∠3=90°，QF=AB=10，
∵六个大小完全一样的小正方形如图放置在大正方形中，
∴∠1+∠2=90°，
∴∠1=∠PQB，
∴△BQP∽△FQN，
∴
=
=
，
∴
=
，
∴QB=2．
∴AF=2．
同理DN=2．
∴NF=AD-DN-AF=6．
∴QN=
=
=2
，
∴小正方形的边长为
，
则六个小正方形的面积和是6×（
）2=
．
故答案为：
．
解：如图所示：∵正方形ABCD边长为10，
∴∠A=∠B=90°，AB=10，
过点Q作QF⊥AD，垂足为F，则∠4=∠5=90°，
∴四边形AFQB是矩形，
∴∠2+∠3=90°，QF=AB=10，
∵六个大小完全一样的小正方形如图放置在大正方形中，
∴∠1+∠2=90°，
∴∠1=∠PQB，
∴△BQP∽△FQN，
∴
| QB |
| QF |
| QP |
| QN |
| 1 |
| 5 |
∴
| QB |
| 10 |
| 1 |
| 5 |
∴QB=2．
∴AF=2．
同理DN=2．
∴NF=AD-DN-AF=6．
∴QN=
| QF2+FN2 |
| 102+62 |
| 34 |
∴小正方形的边长为
2
| ||
| 5 |
则六个小正方形的面积和是6×（
2
| ||
| 5 |
| 816 |
| 25 |
故答案为：
| 816 |
| 25 |
点评：考查了面积及等积变换，本题主要利用相似三角形的判定和相似三角形对应边成比例的性质和勾股定理，综合性较强，有一定的难度．
练习册系列答案
阅读快车系列答案
相关题目
（2013•重庆）如图，在边长为1的小正方形组成的10×10网格中（我们把组成网格的小正方形的顶点称为格点），四边形ABCD在直线l的左侧，其四个顶点A、B、C、D分别在网格的格点上．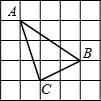
（2012•北海）如图，在边长为1的正方形组成的网格中，△ABC的顶点都在格点上，将△ABC绕点C顺时针旋转60°，则顶点A所经过的路径长为（ ）
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．（直接填写答案）
定义：两个直角三角形，若一个三角形的两条直角边分别与另一个三角形的两条直角边相等，我们就说这两个直角三角形是“同胞直角三角形”．如图，在边长为10的正方形中有两个直角三角形，当直角三角形①和直角三角形②是同胞直角三角形时，a的值是