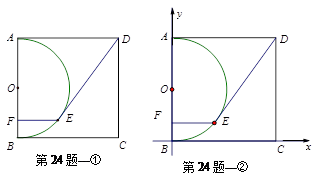
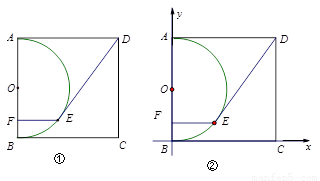
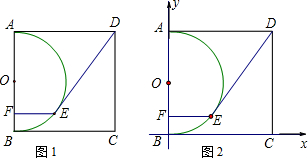
题目内容
在边长为10的正方形ABCD中,以AB为直径作半圆O,如图①,E是半圆上一动点,过点E作EF⊥AB,垂足为F,连接DE.(1)当DE=10时,求证:DE与圆O相切;
(2)求DE的最长距离和最短距离;
(3)如图②,建立平面直角坐标系,当DE=10时,试求直线DE的解析式.
分析:(1)如图1,连接OE,OD,由题意得,DE=DA=10,利用(SSS)判定△AOD≌△EOD,从可得∠OED=∠OAD=90°即可.
(2)当点E运动到与B点重合的位置时,如图2,DE为正方形ABCD的对角线,所以此时DE最长,利用勾股定理求得DE,证明当点E运动到线段OD与半圆O的交点处时,DE最短.然后求得DE=OD-OE即可.
(3)当点E与点A重合时,DE=DA=10,此时,直线DE的解析式为y=10;如图4,当点E与点A不重合时,过点E作GH⊥x轴,分别交AD,x轴于点G,H,连接OE.则四边形AFEG是矩形,且DE为圆O的切线,求证△OFE∽△DGE,利用其对应边成比例,设E(m,n),则有:EF=m,OF=OB-FB=5-n求得即可.
(2)当点E运动到与B点重合的位置时,如图2,DE为正方形ABCD的对角线,所以此时DE最长,利用勾股定理求得DE,证明当点E运动到线段OD与半圆O的交点处时,DE最短.然后求得DE=OD-OE即可.
(3)当点E与点A重合时,DE=DA=10,此时,直线DE的解析式为y=10;如图4,当点E与点A不重合时,过点E作GH⊥x轴,分别交AD,x轴于点G,H,连接OE.则四边形AFEG是矩形,且DE为圆O的切线,求证△OFE∽△DGE,利用其对应边成比例,设E(m,n),则有:EF=m,OF=OB-FB=5-n求得即可.
解答:证明:(1)如图1,连接OE,OD,由题意得,
DE=DA=10,OA=OE=
AB=5,OD为公共边
∴△AOD≌△EOD(SSS)
∴∠OED=∠OAD=90°
∴OE⊥DE,
∴DE与圆O相切.
(2)当点E运动到与B点重合的位置时,如图2,DE为正方形ABCD的对角线,所以此时DE最长,
有:DE=
=10
,
当点E运动到线段OD与半圆O的交点处时,DE最短.
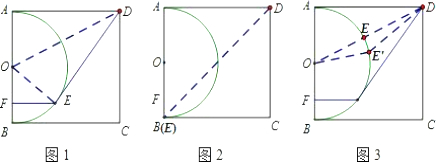
证明如下:
在半圆O上任取一个不与点E重合的点E′,连接OE′,DE′.如图3,
在△ODE′中,∵OE′+DE′>OD即:OE′+DE′>OE+DE,
∵OE′=OE,
∴DE′>DE
∵点E′是任意一个不与点E重合的点,∴此时DE最短.
∴DE=OD-OE=
-OE=
-5=5
-5,
(3)当点E与点A重合时,DE=DA=10,此时,直线DE的解析式为y=10;如图4,
当点E与点A不重合时,过点E作GH⊥x轴,分别交AD,x轴于点G,H,连接OE.
则四边形AFEG是矩形,
连接OD,
∵AD=DE,OA=OE,OD=OD,
∴△AOD≌△EOD,
∴∠OED=90°,
∴DE为圆O的切线
∴∠FEG=∠OED=90°
∴∠FEO=∠GED,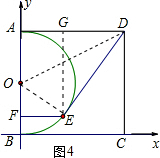
又∵∠OFE=∠DGE=90°
∴△OFE∽△DGE
∴
=
=
,
设E(m,n),则有:EF=m,OF=OB-FB=5-n
得:
=
=
,
解得:
,即:E(4,2)
又直线DE过点D(10,10),设直线DE解析式为y=kx+b,则有:
,
解得:
,即:y=
x-
∴当DE=10时,直线DE的解析式为y=
x-
;
以下两种解法涉及高中知识,仅供参考:
另解2:
(1)当点E与点A重合时,DE=DA=10,此时,直线DE的解析式为y=10;
(2)当点E与点A不重合时,tan∠ADO=
,tan∠ADE=tan2∠ADO=
=
设直线y=
x+b且经过点(10,10),代入求得b=-
所以直线DE的解析式为y=
x-
;
另解3:
依题意得:点O的坐标为(0,5),设直线DE的解析式为y=kx+b
由点到直线的距离公式得:l=
=5,即(b-5)2=25(k2+1)①
直线DE过点D(10,10),得10=10k+b②
由①②解得:75k2-100k=0,解得k=0,k=
所以直线DE的解析式为:为y=
x-
.
DE=DA=10,OA=OE=
| 1 |
| 2 |
∴△AOD≌△EOD(SSS)
∴∠OED=∠OAD=90°
∴OE⊥DE,
∴DE与圆O相切.
(2)当点E运动到与B点重合的位置时,如图2,DE为正方形ABCD的对角线,所以此时DE最长,
有:DE=
| AD2+AB2 |
| 2 |
当点E运动到线段OD与半圆O的交点处时,DE最短.

证明如下:
在半圆O上任取一个不与点E重合的点E′,连接OE′,DE′.如图3,
在△ODE′中,∵OE′+DE′>OD即:OE′+DE′>OE+DE,
∵OE′=OE,
∴DE′>DE
∵点E′是任意一个不与点E重合的点,∴此时DE最短.
∴DE=OD-OE=
| AD2+AO2 |
| 102+52 |
| 5 |
(3)当点E与点A重合时,DE=DA=10,此时,直线DE的解析式为y=10;如图4,
当点E与点A不重合时,过点E作GH⊥x轴,分别交AD,x轴于点G,H,连接OE.
则四边形AFEG是矩形,
连接OD,
∵AD=DE,OA=OE,OD=OD,
∴△AOD≌△EOD,
∴∠OED=90°,
∴DE为圆O的切线
∴∠FEG=∠OED=90°
∴∠FEO=∠GED,

又∵∠OFE=∠DGE=90°
∴△OFE∽△DGE
∴
| OF |
| DG |
| EF |
| EG |
| OE |
| DE |
设E(m,n),则有:EF=m,OF=OB-FB=5-n
得:
| 5-n |
| 10-m |
| m |
| 10-n |
| 5 |
| 10 |
解得:
|
又直线DE过点D(10,10),设直线DE解析式为y=kx+b,则有:
|
解得:
|
| 4 |
| 3 |
| 10 |
| 3 |
∴当DE=10时,直线DE的解析式为y=
| 4 |
| 3 |
| 10 |
| 3 |
以下两种解法涉及高中知识,仅供参考:
另解2:
(1)当点E与点A重合时,DE=DA=10,此时,直线DE的解析式为y=10;
(2)当点E与点A不重合时,tan∠ADO=
| 1 |
| 2 |
| 2tan∠ADO |
| 1-(tan∠ADO)2 |
| 4 |
| 3 |
设直线y=
| 4 |
| 3 |
| 10 |
| 3 |
所以直线DE的解析式为y=
| 4 |
| 3 |
| 10 |
| 3 |
另解3:
依题意得:点O的坐标为(0,5),设直线DE的解析式为y=kx+b
由点到直线的距离公式得:l=
| b-5 | ||
|
直线DE过点D(10,10),得10=10k+b②
由①②解得:75k2-100k=0,解得k=0,k=
| 4 |
| 3 |
所以直线DE的解析式为:为y=
| 4 |
| 3 |
| 10 |
| 3 |
点评:此题涉及到的知识点较多,有相似三角形的判定与性质,待定系数法求一次函数解析式,勾股定理,切线的判定与性质,综合性很强,是一道很典型的题目.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 定义:两个直角三角形,若一个三角形的两条直角边分别与另一个三角形的两条直角边相等,我们就说这两个直角三角形是“同胞直角三角形”.如图,在边长为10的正方形中有两个直角三角形,当直角三角形①和直角三角形②是同胞直角三角形时,a的值是
定义:两个直角三角形,若一个三角形的两条直角边分别与另一个三角形的两条直角边相等,我们就说这两个直角三角形是“同胞直角三角形”.如图,在边长为10的正方形中有两个直角三角形,当直角三角形①和直角三角形②是同胞直角三角形时,a的值是 如图,在边长为10的正方形ABCD中,内接六个大小相同的正方形,P、Q、M、N是落在大正方形边上的顶点.则这六个小正方形的面积和是
如图,在边长为10的正方形ABCD中,内接六个大小相同的正方形,P、Q、M、N是落在大正方形边上的顶点.则这六个小正方形的面积和是