题目内容
15.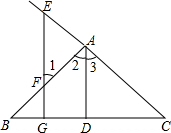 看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠BAC.
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°(垂直的定义)
∴∠ADC=∠EGC(等量代换)
∴AD∥EG(同位角相等,两直线平行 )
∴∠1=∠2(两直线平行,内错角相等)
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1( 已知)
∴∠2=∠3(等量代换)
∴AD平分∠BAC(角平分线的定义).
分析 由垂直可证明AD∥EG,由平行线的性质可得到∠1=∠2=∠3=∠E,可证得结论,据此填空即可.
解答 证明:
∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=90°,∠EGC=90°(垂直的定义),
∴∠ADC=∠EGC(等量代换),
∴AD∥EG(同位角相等,两直线平行 ),
∴∠1=∠2(两直线平行,内错角相等),
∠E=∠3(两直线平行,同位角相等),
又∵∠E=∠1( 已知),
∴∠2=∠3(等量代换),
∴AD平分∠BAC(角平分线的定义).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;等量代换;角平分线的定义.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
10.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标是( )
| A. | (2,2) | B. | (3,3) | C. | (3,2) | D. | (2,3) |
4.-|-2|的相反数的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
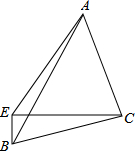 如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.
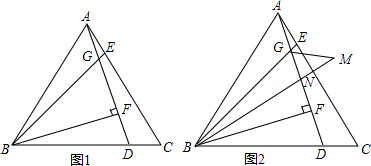
如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.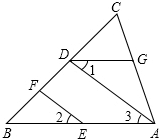 (1)如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
(1)如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.