题目内容
12．在Rt△ABC中，∠C=90°，AC=5cm，BC=12cm，则Rt△ABC其外接圆半径为6.5cm．分析 由勾股定理可求得斜边AB的长，由直角三角形外接圆半径等于斜边长的一半，即可得出结果．
解答 解：∵Rt△ABC中，∠C=90°，AC=5cm，BC=12cm，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13（cm），
∵Rt△ABC中，∠C=90°，
∴AB是其外接圆的直径，
∴其外接圆半径为：$\frac{1}{2}$AB=6.5cm．
故答案为：6.5．
点评 此题考查了直角三角形的外接圆的性质、勾股定理；熟练掌握勾股定理，熟记直角三角形的斜边是其外接圆的直径是解决问题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
7．如果ab＜0，且ac=0，那么直线ax+by+c=0一定通过（ ）
| A． | 第一、三象限 | B． | 第二、四象限 | C． | 第一、二、三象限 | D． | 第一、三、四象限 |
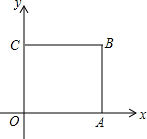如图，在平面直角坐标系中，正方形OABC的一个顶点为B（1，1），点A，C分别在x轴，y轴上．