题目内容
6.如图1,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形如图2.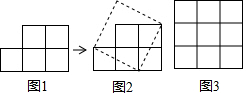
(1)图2中拼成的正方形的边长是$\sqrt{5}$;(填有理数或无理数)
(2)能在3×3方格图(图3)中,连接四个格点(网格线的交点)组成面积为5的正方形吗?若能,请用虚线画出.
(3)在数轴上找到这个数(保留画图痕迹).
分析 (1)直接根据勾股定理即可得出结论;
(2)求出正方形的边长,再由勾股定理画出图形即可;
(3)根据勾股定理在数轴上找出此数即可.
解答  解:(1)正方形的边长=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
解:(1)正方形的边长=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$;
(2)∵正方形的面积为5,
∴其边长为$\sqrt{5}$.
如图1,正方形ABCD即为所求;
(3)如图2,点A表示的数即为$\sqrt{5}$.
点评 本题考查的是图形的拼剪,熟知勾股定理是解答此题的关键.

练习册系列答案
相关题目
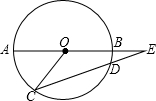 如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.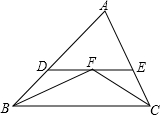 如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
如图,任意△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论: 如图是一个数值转换器,当输入-1时,请计算出输出结果?(要有计算过程)
如图是一个数值转换器,当输入-1时,请计算出输出结果?(要有计算过程)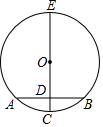 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )