题目内容
7.先化简,再求值:$\frac{1}{x+2}$-$\frac{{x}^{2}-4x+4}{{x}^{2}-x}$÷(x+1-$\frac{3}{x-1}$),其中x满足x(x+2)=2+x.分析 先根据分式混合运算的法则把原式进行化简,再把求出x的值代入进行计算即可.
解答 解:原式=$\frac{1}{x+2}$-$\frac{(x-2)^{2}}{x(x-1)}$÷$\frac{(x+1)(x-1)-3}{x-1}$
=$\frac{1}{x+2}$-$\frac{{(x-2)}^{2}}{x(x-1)}$•$\frac{x-1}{(x+2)(x-2)}$
=$\frac{1}{x+2}$-$\frac{x-2}{x(x+2)}$
=$\frac{2}{{x}^{2}+2x}$,
∵x(x+2)=2+x,
∴x1=1,x2=-2,
当x=-2时原式无意义;
当x=1时,原式=$\frac{2}{1+2}$=$\frac{2}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
17. 如图,扇形AOB的半径为1,∠AOB=90°,连接AB,则图中阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,连接AB,则图中阴影部分的面积为( )
 如图,扇形AOB的半径为1,∠AOB=90°,连接AB,则图中阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,连接AB,则图中阴影部分的面积为( )| A. | $\frac{1}{4}π-\frac{1}{2}$ | B. | $π-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}π$ |
18.已知一组数据x1,x2,x3的平均数为6,则数据x1+1,x2+1,x3+1的平均数为( )
| A. | 6 | B. | 7 | C. | 9 | D. | 12 |
15.以下事件为必然事件的是( )
| A. | 掷一枚质地均匀的骰子,向上一面的点数小于6 | |
| B. | 多边形的内角和是360° | |
| C. | 二次函数的图象不过原点 | |
| D. | 半径为2的圆的周长是4π |
2.下列图形:①平行四边形;②菱形;③圆;④直角三角形;⑤等腰三角形,这些图形中一定是轴对称图形不一定是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
16.甲、乙两地相距270千米,从甲地开出一辆快车,速度为120千米/时,从乙地开出一辆慢车,速度为75千米/时,如果两车相向而行,慢车先开出1小时后,快车开出,那么再经过多长时间两车相遇?若设再经过x小时两车相遇,则根据题意列方程为( )
| A. | 75×1+(120-75)x=270 | B. | 75×1+(120+75)x=270 | ||
| C. | 120(x-1)+75x=270 | D. | 120×1+(120+75)x=270 |
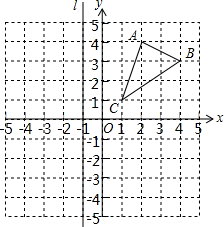 如图,已知△ABC的三个顶点的坐标为:A(2,4),B(4,3),C(1,1),直线l过点(-1,0)且平行于y轴.
如图,已知△ABC的三个顶点的坐标为:A(2,4),B(4,3),C(1,1),直线l过点(-1,0)且平行于y轴.