题目内容
【题目】如图，长方形OABC的边OA，OC在坐标轴上，A（0，2），C（4，0）．点P从点A出发，以每秒1个单位长度的速度沿射线AO方向运动，同时点Q从点C出发，以每秒2个单位的速度沿射线CO方向运动．设点P运动时间为t秒，(t>0)
（1）当t=1时，求△BPQ的周长；
（2）当t为何值时，△BPQ是等腰三角形；
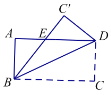
（3）点C关于BQ的对称点为C’，当C’恰好落在直线AQ上时，△BPQ的面积为__________．（直接写出结果）
【答案】（1）
；（2）当
或
或
或
时，
是等腰三角形；（3）
或
．
【解析】
（1）当
时，则
，
，
，
，利用勾股定理可求出
、
、
的长即可；
（2）分三种情形，列出方程即可解决问题；
（3）分两种情形①点
在线段
上时，当
恰好落在直线
上时，
，②点在
的延长线上时，同法可知
，
，利用分割法求的面积即可；
解：（1）∵长方形OABC的边OA，OC在坐标轴上，A（0，2），C（4，0）．
∴OA＝BC＝2，OC＝BA＝4，
∴当时，则，
，，
，
四边形OABC是长方形，
，
，
，
，
的周长
．
（2）由题意可知：
，
，
，
①当
时，
，
化简得：
，
解得
．
③当
时，
，
解得：
或
（都不符合题意，舍去）
②当
时，
，
化简得：，
解得或
，
综上所述，当或或或时，是等腰三角形．
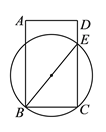
（3）如图2中．
①点在线段上时，当恰好落在直线上时，，
，
，
，
，
在
中，
，
，
，
此时
，
，
，
，
②点在的延长线上时，同法可知，，
此时
，
，，
，
综上所述，当恰好落在直线上时，的面积为或．
练习册系列答案
相关题目
