题目内容
在Rt△ABC中,∠ACB=90°,CD是AB边上的高,则下列结论:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④CD•AD=AC•BC;⑤
=
,正确的个数有( )
| AC2 |
| BC2 |
| AD |
| BD |
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:相似三角形的判定与性质
专题:
分析:直接根据射影定理来分析、判断,结合三角形的面积公式问题即可解决.
解答: 解:如图,∵∠ACB=90°,CD是AB边上的高,
解:如图,∵∠ACB=90°,CD是AB边上的高,
∴由射影定理得:AC2=AD•AB,BC2=BD•AB,
CD2=AD•BD;
∴
=
=
;
∵S△ABC=
AC•BC=
AB•CD,
∴CD•AB=AC•BC,
∴①②③⑤正确,④不正确.
故选C.
 解:如图,∵∠ACB=90°,CD是AB边上的高,
解:如图,∵∠ACB=90°,CD是AB边上的高,∴由射影定理得:AC2=AD•AB,BC2=BD•AB,
CD2=AD•BD;
∴
| AC2 |
| BC2 |
| AD•AB |
| BD•AB |
| AD |
| BD |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD•AB=AC•BC,
∴①②③⑤正确,④不正确.
故选C.
点评:该题主要考查了射影定理及其应用问题;解题的关键是灵活运用射影定理来分析、判断、推理或解答.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

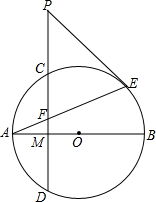 如图,在⊙O中,直径AB与弦CD相交于点M,且M是CD的中点,点P在DC的延长线上,PE是⊙O的切线,E是切点,AE与CD相交于点F,PE与PF的大小有什么关系?为什么?
如图,在⊙O中,直径AB与弦CD相交于点M,且M是CD的中点,点P在DC的延长线上,PE是⊙O的切线,E是切点,AE与CD相交于点F,PE与PF的大小有什么关系?为什么?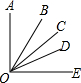 如图,已知OB、OC、OD为∠AOE内三条射线.
如图,已知OB、OC、OD为∠AOE内三条射线.